[Algorithms] Dijkstra Algorithms

Dijkstra Algorithms (다익스트라 알고리즘)

다익스트라 알고리즘은 원래 두 꼭짓점 간 가장 짧은 경로를 찾는 알고리즘이지만 그래프의 한 점에서 연결된 모든 점까지의 최단거리를 구하는 것으로도 사용되는 알고리즘입니다. 이를 최단 경로 트리를 든다고 하죠. 이는 컴퓨터 과학자 에츠허르 다익스트라가 1956년 고안해 3년 뒤 발표했다고 합니다. 논문 링크는 여기

이 과정이 잘 표현된 그림이 wikipedia에 나타나 있습니다. 각 요소는 아래와 같은 뜻을 가집니다.

• 원 안의 숫자: 노드 번호
• 선 위의 숫자: 간선의 길이
• 빨간 숫자: 도달할 수 있는 후보에 등록되지 않은 경우
• 파란 숫자: 해당 위치까지 필요한 최단거리로 예상되는 값

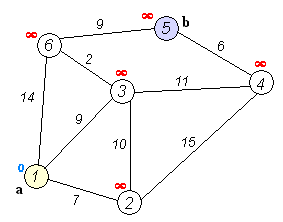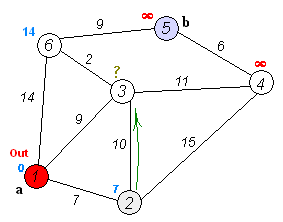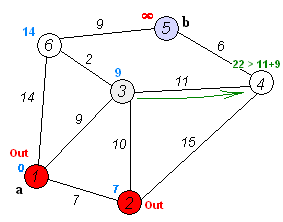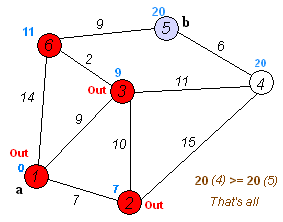
먼저 시작노드 a로부터 인접한 세 노드까지의 거리를 확인합니다. 가장 처음은 모두 $\infty$ 값을 저장하고 있습니다. 그리고 매 step마다 현재 이어질 수 있는 노드들 중 가장 가까운 거리를 만드는 노드로 이동합니다. 이때 가장 가까운 노드를 구하기 위해 우선순위 큐를 활용하는 것이 포인트입니다.

대표적인 문제는 https://www.acmicpc.net/problem/1753 을 풀어보시면 더욱 쉽게 이해할 수 있습니다. 아래는 해당 문제의 소스코드입니다. Time out은 같은 흐름이나 heapq 모듈이 아닌 list를 매 step 마다 정렬하거나 PriorityQueue 모듈을 사용할 때 발생했습니다.

소스코드

import heapq

# input
V, E = map(int, input().split(' '))

# start point
start_node = int(input())

# input
adj_node_list = [[] for _ in range(V + 1)]
for _ in range(E):
    a, b, w = map(int, input().split(' '))

    # add node
    adj_node_list[a].append((b, w))

# dynamic memory
dp = [float('inf') for _ in range(V + 1)]

# bfs
def bfs():
    # initial node
    dp[start_node] = 0

    # priority que
    heap = []
    heapq.heappush(heap, (dp[start_node], start_node))

    while heap:
        # 가장 거리가 짧은 노드
        d, node = heapq.heappop(heap)

        # 인접 노드
        adj_nodes = adj_node_list[node]

        # 인접 노드들을 추가
        for n, w in adj_nodes:
            if dp[n] <= dp[node] + w:
                continue
            else:
                dp[n] = dp[node] + w
                heapq.heappush(heap, (dp[n], n))

    for d in dp[1:]:
        if d is not float('inf'):
            print(d)
        else:
            print('INF')

def main():
    bfs()

if __name__=="__main__":
    main()

Time out 발생하는 코드 1

from queue import PriorityQueue

# input
V, E = map(int, input().split(' '))

# start point
start_node = int(input())

# input
adj_node_list = [[] for _ in range(V + 1)]
for _ in range(E):
    a, b, w = map(int, input().split(' '))

    # add node
    adj_node_list[a].append((b, w))

# dynamic memory
dp = [float('inf') for _ in range(V + 1)]

# bfs
def bfs():
    # initial node
    dp[start_node] = 0

    # priority que
    que = PriorityQueue()
    que.put((dp[start_node], start_node))

    while que.qsize() != 0:
        # 가장 거리가 짧은 노드
        d, node = que.get()

        # 인접 노드
        adj_nodes = adj_node_list[node]

        # 인접 노드들을 추가
        for n, w in adj_nodes:
            if dp[n] <= dp[node] + w:
                continue
            else:
                dp[n] = dp[node] + w
                que.put((dp[n], n))

    for d in dp[1:]:
        print(d)

def main():
    bfs()

if __name__=="__main__":
    main()

Time out 발생하는 코드 2

from collections import deque

# input
V, E = map(int, input().split(' '))

# start point
start_node = int(input())

# input
adj_node_list = [[] for _ in range(V + 1)]
for _ in range(E):
    a, b, w = map(int, input().split(' '))

    # add node
    adj_node_list[a].append((b, w))

# dynamic memory
dp = [float('inf') for _ in range(V + 1)]

# bfs
def bfs():
    # initial node
    dp[start_node] = 0

    # priority que
    que = []
    que.append((dp[start_node], start_node))

    while bool(que):
        que.sort(key=lambda x:x[0])

        # 가장 거리가 짧은 노드
        d, node = que[0]
        del que[0]

        # 인접 노드
        adj_nodes = adj_node_list[node]

        # 인접 노드들을 추가
        for n, w in adj_nodes:
            if dp[n] <= dp[node] + w:
                continue
            else:
                dp[n] = dp[node] + w
                que.append((dp[n], n))

    for d in dp[1:]:
        print(d)

def main():
    bfs()

if __name__=="__main__":
    main()