[Algorithms] Binary Search

Binary search algorithm (이분 탐색 알고리즘)

설명에 앞서 이분 탐색 알고리즘의 핵심은 while 안에 선언되어야 할 변수는 아래 네 가지라는 것입니다. 여기서 가장 중요한 것이 Temporary Answer이며, 반환되는 값은 보통 Index라는 사실입니다.

• Left
• Right
• Middle
• Temporary Answer

탐색 알고리즘 중 하나인 binary search는 half-interval search, logarithmic search 등으로도 불리는 탐색 방법입니다. 이는 검색 대상인 배열이

1. 정렬되어 있을 때
2. 인덱스로 접근 가능할 때

사용합니다. 알고리즘은 다음과 같은 순서로 찾으려는 대상을 탐색합니다. 검색 대상인 배열이 오름차순으로 정렬되어 INDEX가 증가함에 따라 값도 함께 증가한다고 가정하겠습니다.

• 배열의 중간 지점을 선택합니다.
• 만약 선택된 값이 타겟이라면 검색을 멈추고 인덱스를 반환합니다.
• 만약 선택된 값이 타겟보다 크다면 왼쪽 반을 검색합니다.
• 만약 선택된 값이 타겟보다 크다면 오른쪽 반을 검색합니다.
• 더 이상 검색할 원소가 남아있지 않을 때까지 위의 과정을 반복합니다.

이 방법은 최악의 경우 n개의 원소 개수에 대한 logarithmic time인 $O(log{n})$ 시간 효율성 안에 동작할 수 있습니다. 배열의 크기가 작지 않을 때 선형검색보다 빠른 검색 속도를 보여주는 장점이 있지만 정렬된 상태에서만 사용될 수 있다는 제한이 있습니다.

따라서 더 빠른 검색을 위해 고안된 자료구조로 hash table이 있습니다. 그치만 이분 탐색은 단순 타겟을 검색하는 것에서 그치지 않고 여러 곳에서 쓰이는데, 그 예로 lower bound와 upper bound를 구하는 것이 있습니다. 이들은 배열에 타겟이 존재하지 않을 때에도 활용될 수 있습니다.

또한 여러 변형이 존재하며 이전에 포스팅했던 Meet in the middle 알고리즘에서도 이분탐색을 이용해 검색 시간을 줄여 문제를 해결하는 것을 확인할 수 있습니다.

Floor | Ceil | Round

알고리즘을 본격적으로 알아보기 전에 위 함수에 대한 개념을 짚고 넘어가면 좋을 것 같습니다. 저는 이들의 개념은 대략 알고있으나 정확하게 활용하기 어려웠었습니다. 사실 뜻을 이해하고 있다면 암기할 필요없이 활용할 수 있을 것입니다.

• Floor: 바닥입니다. 어떠한 값이든 바닥으로 붙이는 것이라고 생각하면 편합니다. 간단한 예로 0.9라는 소수값에 floor()를 취하면 0값을 반환합니다.
• Ceil: 천장입니다. 어떠한 값이든 천장으로 붙이는 것이라고 생각하면 편합니다. 간단한 예로 0.1이라는 소수값에 ceil()을 취하면 1값을 반환합니다.
• Round: 우리가 잘 아는 반올림입니다. 감다라는 뜻을 가지고 있습니다. 더 가까운 곳으로 감는다 이해하면 편할 것 같습니다.

이분탐색에서 floor와 ceil이 중요한 이유는 다음과 같습니다. 홀수개의 원소가 존재할 때는 어떤 경우라도 가운데를 가리키지만 짝수 개일 때는 아래와 같이 동작합니다.

알고리즘 순서

일반적인 경우

이분탐색은 이를 활용하려는 목적에 따라 구현이 조금씩 달라집니다. 먼저 가장 간단하게 서로 다른 값으로 이루어진 배열에서 특정한 값을 찾는 경우입니다. 여기서 서로 다른 값으로 이루어진 배열은 임의의 $T$에 대하여 $T$가 오로지 배열에 한 개만 존재한다는 것을 보장합니다.

길이 $n$인 배열 $A$의 원소는 다음과 같이 $A_0 < A_1 < … < A_{n-1}$ 으로 구성되어있습니다. 찾으려는 원소 $T$에 대해 다음과 같은 과정을 거쳐 배열을 탐색합니다.

1. $L$에 0, $R$에 n-1 값을 할당합니다.
2. if $L > R$ 이면 탐색하려는 값이 배열에 없는 것으로 탐색을 종료합니다.
3. $m$ 의 값에 $floor(\frac{L + R}{2})$ 을 할당합니다.
4. if $A_m < T$ 라면 $L$ 에 $m+1$ 값을 대입하고 2번으로 이동합니다.
5. if $A_m > T$ 라면 $R$ 에 $m-1$ 값을 대입하고 2번으로 이동합니다.
6. $A_m = T$ 라면 m을 반환하고 탐색을 종료합니다.

이를 psuedo code로 나타내면 아래와 같습니다.

function binary_search(A, n, T) is
    L := 0
    R := n − 1
    while L ≤ R do
        m := floor((L + R) / 2)
        if A[m] < T then
            L := m + 1
        else if A[m] > T then
            R := m − 1
        else:
            return m
    return unsuccessful

위의 경우에서는 3번 순서에서 $ceil(\frac{L + R}{2})$을 대입해도 같은 답을 얻을 수 있습니다. 위 알고리즘의 특징으로는 $L$과 $R$을 $m+1$과 $m-1$로 업데이트한다는 것에 있습니다. 한 번의 Loop에서 3번의 비교를 통해 $A_m = T$인 경우를 검사하기 때문에 $m$을 후보에서 제외할 수 있습니다.

일반 경우에서 연산을 줄이는 방법

그렇다면 중간 비교 과정에서 연산 3번을 2번으로 줄일 수 있을까요. 바로 $=$ 비교를 한 가지에 포함하는 것입니다. 한 번의 비교에서 $A_m \le T$라면 $A_x = T$인 $x$이 가능한 범위는 $m \le x \le R$ 이 됩니다. 따라서 $L$은 $m+1$로 업데이트 되는 것이 아니라 $m$으로 업데이트 됩니다.

1. $L$에 0, $R$에 n-1 값을 할당합니다.
2. While $L \ne R$
   1. $m$ 의 값에 $ceil(\frac{L + R}{2})$ 을 할당합니다.
   2. if $A_m > T$ 라면 $R$ 에 $m-1$ 값을 대입하고 2번으로 이동합니다.
   3. if $A_m \le T$ 라면 $L$ 에 $m$ 값을 대입하고 2번으로 이동합니다.
3. $L = R$ 라면 검색이 종료된 것입니다. $A_L = T$이면 $L$을 반환하고 아닌 경우 값이 존재하지 않는 것입니다.

function binary_search_alternative(A, n, T) is
    L := 0
    R := n − 1
    while L != R do
        m := ceil((L + R) / 2)
        if A[m] > T then
            R := m − 1
        else:
            L := m
    if A[L] = T then
        return L
    return unsuccessful

타겟 값이 배열에 여러 개가 존재할 때

중요한 것은 서로 다른 값으로 이루어진 경우라는 것입니다. 만약 서로 다른 값이 아닌 같은 값이 존재한다면 위 알고리즘은 경우에 따라 다른 결과를 나타냅니다. 탐색 목표 값을 가진 원소가 배열에 여러 개 존재할 때를 가정합니다.

주어진 $[1, 2, 3, 4, 4, 5, 6, 7]$ 이고 $4$가 검색 타깃이라고 할 때, INDEX 2와 INDEX 3 모두 정답이 됩니다. 이럴 때, left most와 right most를 구하는 것은 매우 편리합니다. left most와 rigth most 값을 이용해 같은 값을 가지는 타깃이 몇 개인지 확인할 수도 있습니다.

그러나 많은 분들이 그랬고 저 역시도 상황에 따른 이분탐색을 구현하는데 많은 어려움이 있었습니다. 그래서 가장 중요하게 생각해야하는 것 다섯 가지 포인트를 정리했습니다. 진행과정에서 고려할 것은 다음과 같습니다.

• 종료 조건을 $L < R$로 나타냅니다.
• floor() 를 통해 $L$과 $R$이 붙어 $R = L + 1$인 상태일 때 $m$ 이 $L$의 위치를 가리키도록 합니다.
• $L \larr m + 1$을 통해 종료를 보장합니다.
• 가장 간단한 형태를 가정합니다.
• 어떤 값을 Return할 것인지 결정합니다.

먼저 여러 개의 값들 중 left most를 찾아보겠습니다. 먼저 가장 간단한 형태를 가정함으로써 분기문을 어떻게 작성할지 생각해볼 수 있습니다.

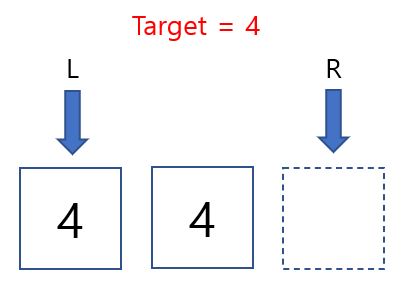
해당 상태에서 가장 처음 가리키는 곳은 1번 INDEX의 4가 있는 곳입니다. 만약 left most를 구하고 싶다면 어떻게 해야할까요? $R$이 움직여야 합니다. 따라서 $A_m$이 $T$일 때, $R$이 움직이도록 $T < A_m$ 분기문에 $=$을 붙여줍니다. 이때 과정은 다음과 같습니다.

1. $L$에 0, $R$에 n 값을 할당합니다.
2. While $L \ne R$
   1. $m$ 의 값에 $floor(\frac{L + R}{2})$ 을 할당합니다.
   2. if $A_m \ge T$ 라면 $R$ 에 $m$ 값을 대입하고 2번으로 이동합니다.
   3. if $A_m < T$ 라면 $L$ 에 $m + 1$ 값을 대입하고 2번으로 이동합니다.
3. $L$을 반환합니다.

마지막으로 어떤 값을 반환할 것인지 생각하면 됩니다. 이를 코드로 나타내면 아래와 같습니다.

function binary_search_leftmost(A, n, T):
    L := 0
    R := n
    while L < R:
        m := floor((L + R) / 2)
        if A[m] < T:
            L := m + 1
        else:
            R := m
    return L

반대로 right most를 구하려면 어떻게 해야할까요? $A_m$이 $T$일 때, $L$이 움직여야 합니다. 따라서 $A_m$이 $T$일 때, $L$이 움직이도록 $T > A_m$ 분기문에 $=$을 붙여줍니다. 이때 과정은 다음과 같습니다.

1. $L$에 0, $R$에 n 값을 할당합니다.
2. While $L \ne R$
   1. $m$ 의 값에 $floor(\frac{L + R}{2})$ 을 할당합니다.
   2. if $A_m > T$ 라면 $R$ 에 $m$ 값을 대입하고 2번으로 이동합니다.
   3. if $A_m \le T$ 라면 $L$ 에 $m + 1$ 값을 대입하고 2번으로 이동합니다.
3. $R-1$을 반환합니다.

이번에도 역시 마지막으로 어떤 값을 반환할 것인지 생각하면 됩니다. 이를 코드로 나타내면 아래와 같습니다.

function binary_search_rightmost(A, n, T):
    L := 0
    R := n
    while L < R:
        m := floor((L + R) / 2)
        if A[m] > T:
            R := m
        else:
            L := m + 1
    return R - 1

근접값

위의 과정은 배열에 정확하게 대응되는 값이 존재할 때를 가정하고 수행됩니다. 그러나 이외에도 여러가지 값을 구하는 데 사용될 수 있습니다. 위에서 배운 알고리즘을 이용해 다음을 구할 수 있습니다.

• Rank: 목표 값보다 작은 원소의 개수. left most를 찾는 과정을 통해 찾을 수 있습니다.
• Predecessor: 목표 값보다 작은 최대 값으로 직전 원소를 뜻합니다. left most INDEX가 타겟 값과 같다면 INDEX - 1 (INDEX > 1)이 가리키는 값이 됩니다.
• Successor: 목표 값보다 큰 최소 값으로 직후 원소를 뜻합니다. right most INDEX가 타겟 값과 같다면 INDEX + 1 (INDEX < N - 1)이 가리키는 값이 됩니다.
• Nearest neighbor: Predecessor와 Successor 중 목표 값과 더 가까운 값을 말합니다.
• 이러한 값들을 이용해 배열의 특정 범위에 편리하게 접근할 수 있으며, 포함 또는 배제를 구현할 수 있습니다.