[Algorithms] Bellman-Ford

Bellman-Ford Algorithms (벨만-포드 알고리즘)

벨만-포드 알고리즘은 음의 가중치를 포함하는 그래프에서 최단 경로 문제를 푸는 알고리즘입니다. 이전에 남겼던 다익스트라 알고리즘과는 다르게 음수의 가중치가 포함된 경우에도 최단거리를 구해낼 수 있습니다.

다음 블로그에서는 벨만-포드 알고리즘이 Greedy Algorithm (그리디 알고리즘) 이 아님을 설명하기 위해 아래와 같이 짧게 정리된 정의를 적었습니다.

A greedy algorithm is any problem-solving heuristic that tries to find the local optimal solution at the time, hoping that at the end, these local optimal solutions will lead to a globally optimal solution

그리디 알고리즘이란 휴리스틱, 인간 직관을 활용한 최적의 지협적 답안이 곧 모든 경우에 적용될 때에도 답이 되는 것을 가정한 알고리즘입니다.

벨만-포드 알고리즘 풀이 과정을 제가 이해한 바로 적으면 다음과 같습니다. 주어진 노드가 모두 N개라고 가정해보겠습니다.

• step 1: 단방향 또는 양방향 인접 노드를 입력
• step 2: 출발점에서부터 거리를 기록하는 dp 선언하고 모든 값을 최대값으로 초기화
• step 3: 출발지 dp[start_point] = 0 으로 설정
• step 4: N회 Loop (N-1 길이의 MST와 Negative cycle 검사 1회)
  • step 4-1: N개의 노드별로 인접 노드 탐색
    • 4-1-1: 인접 노드의 dp 값이 수정되는지 검사
    • 4-1-2: Negative cycle 검사 loop에서 수정되는 노드가 있는지 확인
• step 5: 조건에 따른 정답 출력

아래 그림은 이 과정을 시각적으로 표현한 것으로 출처는 이곳입니다.

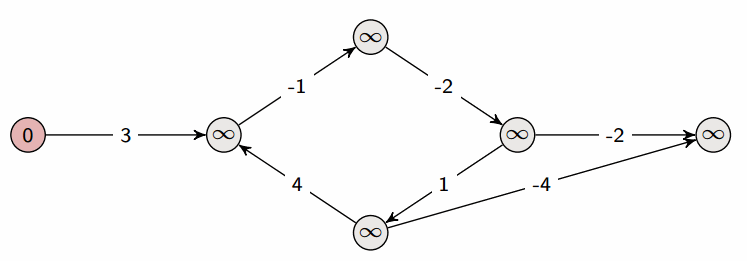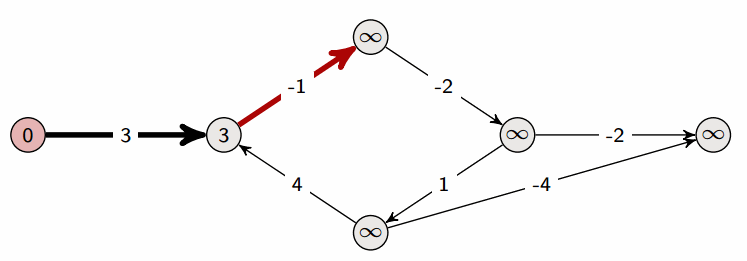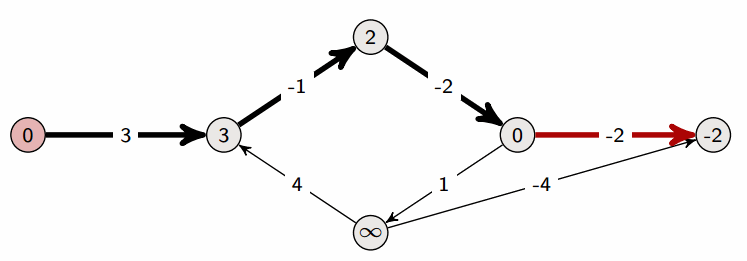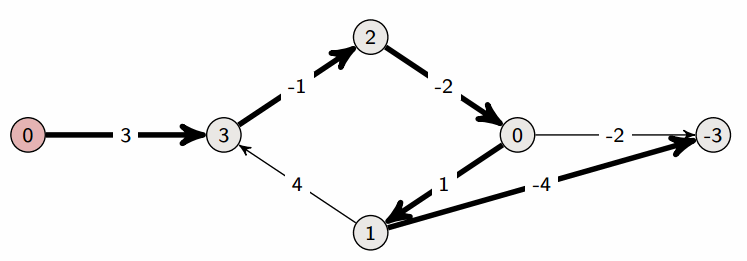
이를 이용해서 풀어볼 수 있는 문제가 두 가지 있습니다. 백준 11657번: 타임머신과 백준 1865: 웜홀 입니다. 저는 항상 float('inf') 를 사용했었으나 2<<31을 이용해서도 최대값을 설정할 수 있음을 배웠습니다.

전자에서는 음수 간선이 존재해도 무한의 값이 변화하지 않아 출발지점을 지정하지 않으면 그래프 변화가 유발되지 않습니다. 따라서 웜홀 문제를 풀 때 Negative cycle을 확인하기 위해 정수 값을 가지는 INF를 따로 선언하는 것이 좋습니다. 아래는 해당 문제들의 소스코드입니다.

소스코드

아래는 문제 풀이에 사용한 소스코드입니다.

백준 11657번: 타임머신

# 도시 개수, 간선 개수
N, M = map(int, input().split(' '))

# 간선 입력
adj_node_list = [[] for _ in range(N + 1)]
for _ in range(M):
    A, B, C = map(int, input().split(' '))
    adj_node_list[A].append((B, C))

def main():
    global N, adj_node_list

    dp = [float('inf') for _ in range(N + 1)]
    dp[1] = 0

    for turn in range(N):
        for current_node in range(1, N+1):
            # 인접 노드
            adj_nodes = adj_node_list[current_node]

            # 인접 노드별로 옆 노드와 최소 거리 갱신
            for next_node, w in adj_nodes:
                if dp[current_node] + w < dp[next_node]:
                    # 갱신 가능할 때
                    dp[next_node] = dp[current_node] + w

                    # 무한루프
                    if turn == N-1:
                        dp[next_node] = -float('inf')
                else:
                    continue

    if -float('inf') in dp:
        print(-1)
    else:
        for d in dp[2:]:
            if d == float('inf'):
                print(-1)
            else:
                print(d)

if __name__=="__main__":
    main()

백준 1865번: 웜홀

# 테스트 케이스
T = int(input())

for test_case in range(1, T + 1):
    INF = 2<<31

    # 입력
    N, M, W = map(int, input().split(' '))

    adj_node_list = [[] for _ in range(N+1)]
    dp = [INF for _ in range(N + 1)]

    for _ in range(M):
        S, E, T = map(int, input().split(' '))
        adj_node_list[S].append((E, T))
        adj_node_list[E].append((S, T))

    for _ in range(W):
        S, E, T = map(int, input().split(' '))
        adj_node_list[S].append((E, -T))

    possible_flag = False
    for turn in range(1, N + 1):
        for current_node in range(1, N+1):
            for next_node, w in adj_node_list[current_node]:
                if dp[current_node] + w < dp[next_node]:
                    # 값 갱신
                    dp[next_node] = dp[current_node] + w

                    if turn == N:
                        possible_flag = True

    if possible_flag:
        print('YES')
    else:
        print('NO')