[Algorithm Problem] 부분합 (BAEKJOON: 1806번)

Subtotal (부분합)

이 문제는 10,000 이하의 자연수로 이루어진 길이 N$(10 \le N \le 100,000)$짜리 수열에서 연속된 수들의 부분합이 S$(0 < S \le 100,000,000)$ 이상이 되는 것들 중 가장 짧은 길이를 구하는 것입니다. 이때 주목할 점은 문제에서 주어진 시간 제한이 C++ 기준 0.5초라는 것입니다.

처음엔 간단한 투 포인터 문제로 생각했으나 번번히 시간초과로 통과하지 못 했습니다. 시간을 더 단축할만한 곳을 찾던 중 부분합의 크기를 구할 때 사용하는 for문을 대신하여 이전 부분합 정보를 이용하는 방법을 떠올렸습니다.

소스코드

계속된 시간초과로 먼저 C++를 시도해보았으나 같은 알고리즘에 대해서 시간초과를 띄웠습니다. 그러나 이전 부분합 값을 활용하여 실행시간을 대폭 줄일 수 있었습니다. 이러한 방법은 각 배열에 0 ~ INDEX 까지 합을 저장한 후 활용하는 방법으로도 응용될 수 있습니다.

아래와 같은 정수 배열이 있다고 가정하겠습니다.

이 배열의 0 ~ INDEX 배열까지 합은 아래 그림과 같이 나타낼 수 있습니다.

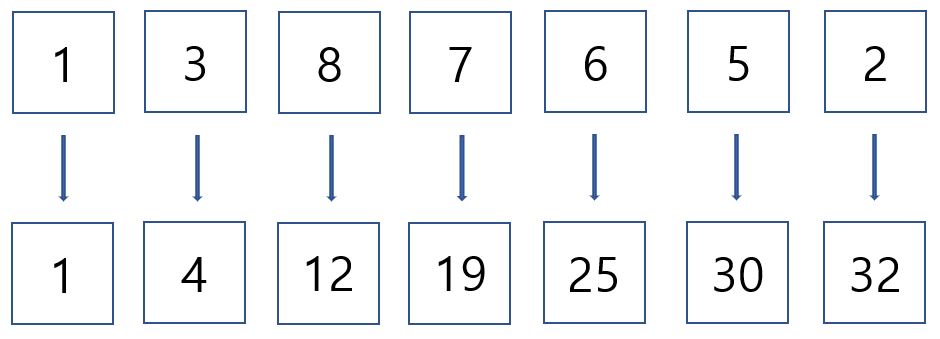
이러한 누적합을 구해놓으면 다음과 같은 이점이 있습니다.

• 한 번의 for문으로 아래 누적합 배열을 만들 수 있습니다.
• 특정 범위에 해당하는 부분합을 for문을 돌지 않고 구할 수 있습니다.

즉, 공간적인 이득은 조금 떨어지나 배열이 커질 수록 연산속도 측면에서 큰 이득을 얻을 수 있습니다. 예를들어, 1번 인덱스에서 5번 인덱스까지의 합을 구하려고 할 때, arr[5] - arr[0] = 29 (3 + 8 + 7 + 6 + 5 = 29)를 for문을 돌지 않고 알아낼 수 있습니다.

위와 같은 부분합 방식을 적용한 코드는 아래와 같습니다. 먼저 C++ 소스코드입니다.

#include <iostream>
#include <algorithm>

using namespace std;

#define MAXNUM 100001 

int arr[100000];
int answer = MAXNUM;

bool compare(int a, int b)
{
	return a < b;
}

int main(int argc, char* argv[])
{
	ios_base::sync_with_stdio(false);
	cin.tie(NULL);

	int N, S, num;

	// 입력
	cin >> N >> S;
	for (int i = 0; i < N; i++)
	{
		cin >> num;
		arr[i] = num;
	}

	// two pointer
	int start_pointer = 0;
	int end_pointer = 0;
	int partial_sum = arr[start_pointer];

	// answer
	while (end_pointer < N)
	{	
		// 부분 합 구하기
		if (partial_sum < S)
		{
			end_pointer += 1;
			partial_sum += arr[end_pointer];
		}
		else
		{
			answer = min(answer, end_pointer - start_pointer + 1);
			partial_sum -= arr[start_pointer];
			start_pointer += 1;
		}
	}

	if (answer == MAXNUM) cout << 0;
	else cout << answer;

	return 0;
}

다음은 Python 소스코드입니다.

if __name__=="__main__":
    N, S = map(int, input().split(' '))

    # index error 방지용 [0]
    num_list = list(map(int, input().split(' '))) + [0]

    start_pointer = 0
    end_pointer = 0
    partial_sum = num_list[start_pointer]

    answer = 2 << 31

    while end_pointer < N:
        if partial_sum < S:
            end_pointer += 1
            partial_sum += num_list[end_pointer]
        else:
            answer = min(answer, end_pointer - start_pointer + 1)
            partial_sum -= num_list[start_pointer]
            start_pointer += 1

    if answer == 2 << 31:
        print(0)
    else:
        print(answer)