[Algorithm Problem] 카드 구매하기 (BAEKJOON: 11052번)

Purchasing Cards (카드 구매하기)

이 문제는 펠린드롬? 문제가 아무리해도 풀리지 않아 Dynamic Programming 문제를 다시 한 번 환기시킬 겸 풀어본 문제입니다. 이전 Knapsack 문제와 비슷하게 풀 수 있을 것 같았으나, N의 값이 1,000을 넘어가기 때문에 Meet in the middle로는 풀 수 없을 것 같았습니다. 또한 원소를 중복사용하는 방법도 있기 때문에 다른 접근법이 필요했습니다.

제가 처음 Knapsack 문제를 접했을 때 배웠던 고전적인 이차원 배열로의 반복적 접근을 통해 문제를 풀어보았습니다. 동적 계획법의 특징은 한 가지 문제를 풀기 위해 같은 형태의 부분 문제를 풀어 해결하는 것 이라고 합니다. 그렇기에 많은 동적 계획법 문제들이 점화식의 형태를 가지고 있습니다.

이 문제 역시 사용할 수 있는 카드 패키지를 순차적으로 증가시키며 그 최대값을 구하였습니다. 현재 사용할 수 있는 카드 패키지로 최대값을 계산할 때, 이전 단계에서 도출해낸 각 카드 개수에 따른 최대값을 활용해 문제를 해결합니다.

가장 처음 형태는 아래와 같습니다. 아무 카드도 선택하지 않았기 때문에 모든 행을 0으로 초기화 시킵니다. 이렇게 하면 점화식에서 특별한 예외처리를 하지 않고도 최대값을 계산할 수 있기 때문에 다음과 같은 형태로 나타냈습니다.

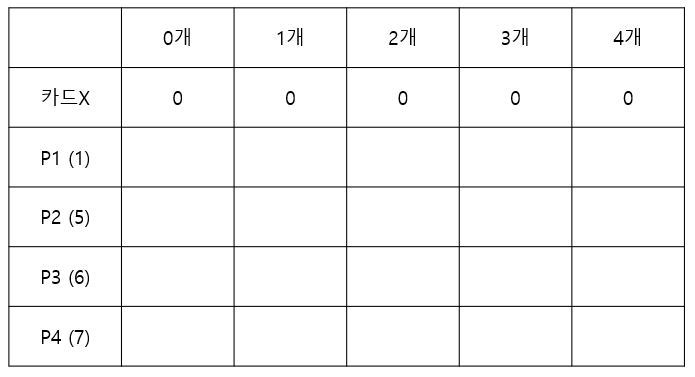
P1은 1장짜리 패키지로 가격은 1원입니다. 1장짜리 패키지를 이용해 총 카드 개수 0개를 만들면 그 가격의 합은 0원입니다. 1개 짜리 카드팩을 만들 때, 이전에 만들었던 카드팩의 가격과 현재 살 수 있는 카드패키지 장 수를 빼고 다른 패키지를 넣었을 때의 가격을 비교해 더 높은 값을 대입합니다. 아래와 P1만으로 카드 2개짜리 팩을 만들 때를 생각해보겠습니다.

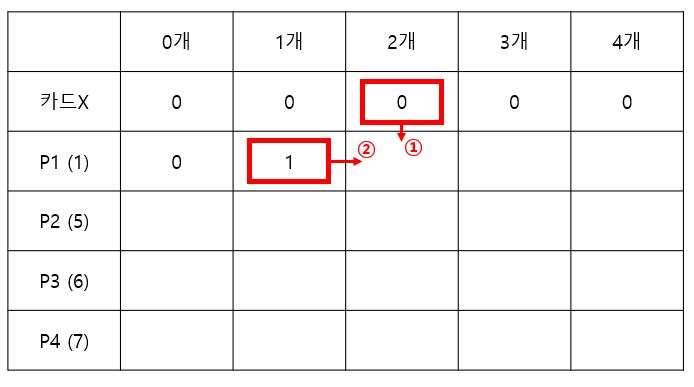
1번의 경우 이전에 만들어 둔 2장짜리 카드팩의 최대 값을 뜻합니다. 이전에 만들어둔 2장짜리 카드팩은 없으므로 1번은 0원 입니다. 2번은 2장짜리 카드팩을 만들 때, 1장짜리 카드팩의 최대 가격에서 1장짜리 패키지를 더 구매해 2장을 만드는 경우를 나타냅니다. 이 경우 값은 2원이 되어 최대값은 2원이 됩니다.

이와 같은 방식으로 P1만을 사용했을 때 최종적으로 4장의 카드팩을 만들 때 최대값은 다음과 같이 4원이 됩니다.

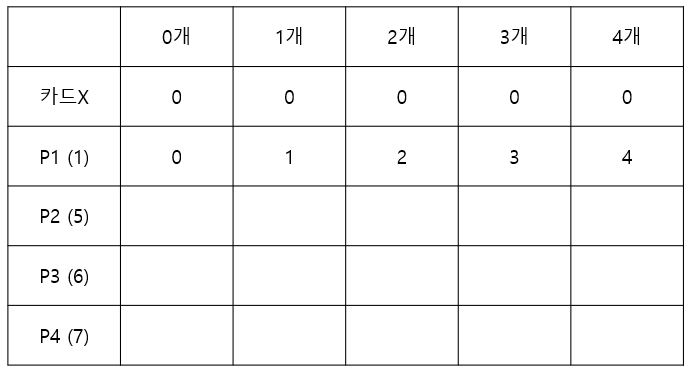
이제 P2 2장짜리를 이용해 최대 가격을 갱신해보겠습니다. P2를 이용해 카드 0개, 카드 1개짜리 팩을 만드는 방법은 이전에 만들어 둔 것을 그대로 가져오는 것입니다. 카드 2개짜리 팩을 만드는 경우는 아래와 같습니다.

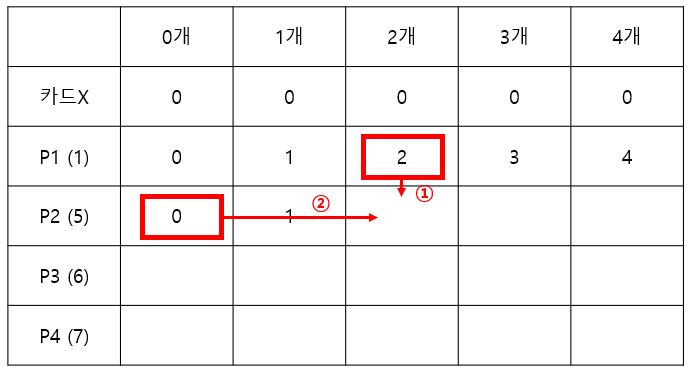
1번은 이전에 만들어두었던 2장짜리 팩을 그대로 가져오는 경우입니다. 2번은 1장짜리 패키지 2개로 구성된 것이 아니라 2장짜리 패키지 하나로 구성할 때의 경우를 나타냅니다. 둘 중 최대값은 5원이 되어 해당 칸의 값은 5가 됩니다. 이러한 방식으로 최대값을 채워나가면 최종적으로 아래와 같은 표가 만들어집니다.

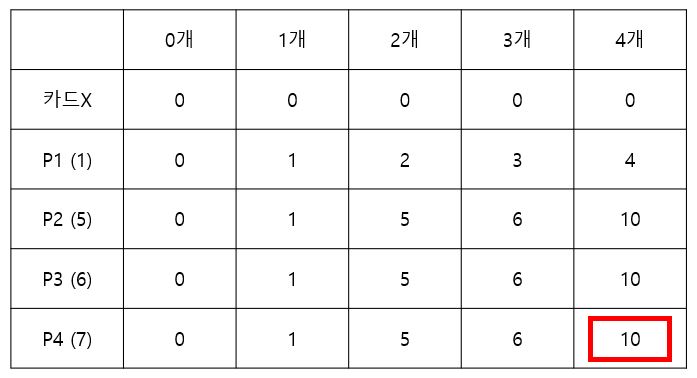
이 패턴을 이용하여 다른 여러 문제를 풀어보면 이해에 도움이 될 것이라 확신합니다.

소스코드

if __name__=="__main__":
    # 개수
    N = int(input())

    # 카드 패키지
    card_p = [0] + list(map(int, input().split(' ')))

    # DP
    dp = [[0 for i in range(N+1)] for j in range(N + 1)]

    for card_num in range(1, N+1):
        for p in range(N + 1):
            if card_num - p < 0:
                # 새로운 카드를 사용할 수 없을 때
                dp[p][card_num] = dp[p-1][card_num]
                continue

            # 현재 카드를 버리고 새로운 카드를 넣었을 때
            dp[p][card_num] = max(dp[p-1][card_num], dp[p][card_num - p] + card_p[p])

    # 최대 값
    print(dp[N][N])