[Algorithm Problem] 경찰차 (BAEKJOON: 2618번)

Police Car (경찰차)

경찰차(BAEKJOON: 2618번) 문제를 푸는데 2주가 걸렸네요. 그마저도 마지막엔 풀이를 확인하면서 풀었습니다. 보기엔 간단했으나 발상이 매우 까다로운 문제였습니다.

문제

• 어떤 도시의 중심가에 N개의 동서방향 도로와 N개의 남북방향 도로가 있습니다.
• 모든 도로에는 1부터 N까지 도로 번호가 부여됩니다.
• 각 도로의 길이는 1입니다.
• 교차점은 정수 쌍으로 나타냅니다.
• 도시에는 경찰차 2대가 있으며, 초기 위치는 (1, 1) 과 (N, N) 입니다.
• 순차적으로 발생하는 사건에 대해서 한 사건은 경찰차 한 대에만 할당할 수 있습니다.
• 모든 사건이 주어졌을 때, 다음을 출력하는 것이 목표입니다.
  • 모든 사건을 해결하는 최소한의 거리
  • 각 사건마다 어떤 경찰차를 출동해야하는가

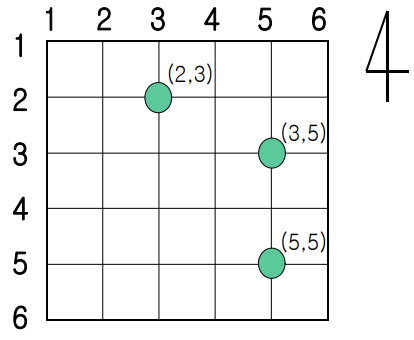
예제 입력

6
3
3 5
5 5
2 3

예제 출력

9
2
2
1

풀이

아래는 풀이에 필요한 몇 가지 정보를 적은 필기입니다.

Dynamic Programming 에서 Memoization 을 이용해 연산 시간을 단축했습니다. 이 과정에서 한 가지를 배웠습니다. 바로 어디서 답을 구할 것인가?를 생각하며 점화식을 설계해야 풀이에 다양성을 적용할 수 있다는 것입니다.

동적 프로그래밍에서 답은 다음과 같이 세 군데에서 발생할 수 있을 것 같습니다.

• 탐색 시작 지점: 현재 문제가 대표적인 예일 것 같습니다. 최소 값을 비교하는 과정에서 다시 한 번 재귀가 발생하며, 모든 경우를 탐색하고, 종료 조건에서 값들을 반환 받으며 마지막에 가장 처음 입력으로 주었던 값을 정답으로 사용합니다.
• 탐색 중간 지점: 탐색 중간에 조건을 만족하는 경우 전역 변수인 Answer를 업데이트합니다. 그리고 이 조건에 의해 Prunning을 할 수 있습니다. 백트래킹 문제에서 많이 사용되는 풀이 방법입니다.
• 탐색 종료 지점: Knapsack 문제 형태가 이와 비슷합니다. for문 을 통해 순차적으로 점화식을 진행시키며 최종 값을 답으로 사용하는 경우입니다.

이러한 세 가지 경우를 생각하며 함수를 설계하면 체계적이면서도 다양한 경우를 고려하며 문제를 해결할 수 있을 것 같습니다.

문제를 보고 가장 먼저 떠오르는 방법은 Greedy 방법이었습니다. 순차적으로 주어지는 사건들의 위치에 따라 더 가까운 자동차를 출동시키는 것입니다. 그러나 같은 거리에 대한 조건을 고려하지 못하니 당연히 틀린 답을 출력했습니다.

두 번째로 시도해 본 방법은 dfs() 를 이용해 모든 경우를 탐색하며 해당 위치에 대한 값을 Cache 에 저장하여 사용하는 것입니다. 9%의 정답률까지 보였으나 틀린 답을 띄웠습니다. 아래는 그 오답 코드입니다.

from collections import deque

def dfs(idx):
    global num_list, distance, route, answer, answer_route, distance, DP

    if idx == len(num_list):
        if answer > distance:
            answer = distance
            answer_route = list(route)
        return

    # check position and distances
    # add car1 state
    distance += abs(car1[0] - num_list[idx][0]) + abs(car1[1] - num_list[idx][1])
    route.append(1)

    if distance < DP[idx]:
        # change car position
        origin_x, origin_y = car1[0], car1[1]
        car1[0], car1[1] = num_list[idx][0], num_list[idx][1]
        dfs(idx + 1)
        car1[0], car1[1] = origin_x, origin_y

        # check distance at the idx
        DP[idx] = distance

    # change to origin
    distance -= abs(car1[0] - num_list[idx][0]) + abs(car1[1] - num_list[idx][1])
    route.pop()

    # add current state
    distance += abs(car2[0] - num_list[idx][0]) + abs(car2[1] - num_list[idx][1])
    route.append(2)

    if distance < DP[idx]:
        # change car position
        origin_x, origin_y = car2[0], car2[1]
        car2[0], car2[1] = num_list[idx][0], num_list[idx][1]
        dfs(idx + 1)
        car2[0], car2[1] = origin_x, origin_y

        # check distance at the idx
        DP[idx] = distance

    # change to origin
    distance -= abs(car2[0] - num_list[idx][0]) + abs(car2[1] - num_list[idx][1])
    route.pop()

def solution():
    global num_list, car1, car2, distance, route, answer, answer_route, DP

    N = int(input())

    W = int(input())

    num_list = []
    DP = [float('inf') for i in range(W)]
    for _ in range(W):
        a, b = map(int, input().split(' '))
        num_list.append((a, b))

    # car positions
    car1 = [1, 1]
    car2 = [N, N]

    # total distance and route
    distance = 0
    route = deque()

    # answers
    answer = 12345678910
    answer_route = []

    # search
    dfs(0)

    # print answer
    print(answer)
    for i in answer_route:
        print(i)

if __name__ == "__main__":
    solution()

마지막은 문제를 푼 많은 분들이 사용한 방법입니다. 먼저 Cache[x][y] 값을 경찰차A가 x번째, 경찰차B가 y번째 사건을 풀었을 때, 남아있는 최소 거리 라는 조금 난해한 정의로 설정합니다. 이렇게 되면 다음 사건번호 NEXT는 NEXT = max(x, y) + 1로 나타낼 수 있습니다.

탐색 방법은 A를 출동시켜본 값과 B를 출동시켜본 값 중 남은 거리가 최소가 되는 값 을 대입하는 방식으로 진행됩니다. 이 과정에서 계속된 재귀가 발생하게 됩니다. 그리고 종료 조건에 달하면 남은 거리 = 0에 의해 0을 반환하며 재귀 식이 풀리게 됩니다.

경로추적은 완성해놓은 DP Cache를 이용해 A와 B를 출동시켰을 때, 최소 값까지 남은 거리가 더 짧은 쪽을 선택하며 진행시킵니다.

정답 코드는 다음과 같습니다.

def dist(car_pos_x, car_pos_y, work_num):
    return abs(car_pos_x - works[work_num][0]) + abs(car_pos_y - works[work_num][1])

def print_cache():
    for i in range(W + 1):
        for j in range(W + 1):
            print(DP[i][j],end=' ')
        print()

def trace_route(a, b):
    if a == W or b == W:
        return

    # next work num
    next_work = max(a, b) + 1

    # car1 distance for next work number
    if a == 0:
        dist1 = dist(1, 1, next_work)
    else:
        dist1 = dist(works[a][0], works[a][1], next_work)

    # car2 distance for next work number
    if b == 0:
        dist2 = dist(N, N, next_work)
    else:
        dist2 = dist(works[b][0], works[b][1], next_work)

    if DP[next_work][b] + dist1 < DP[a][next_work] + dist2:
        # car1 출동할 때 남은 거리가 더 짧음
        print(1)
        trace_route(next_work, b)
    else:
        # car2 출동할 때 남은 거리가 더 짧음
        print(2)
        trace_route(a, next_work)

    return

def dfs(a, b):
    # last case
    if a == W or b == W:
        return DP[a][b]

    # if exist
    if DP[a][b] != float('inf'):
        return DP[a][b]

    # 다음 사건 번호
    next_case = max(a, b) + 1

    # 차량1 위치
    if a == 0:
        car1_x, car1_y = 1, 1
    else:
        car1_x, car1_y = works[a]

    # 차량2 위치
    if b == 0:
        car2_x, car2_y = N, N
    else:
        car2_x, car2_y = works[b]

    # result
    DP[a][b] = min(dfs(next_case, b) + dist(car1_x, car1_y, next_case),
                   dfs(a, next_case) + dist(car2_x, car2_y, next_case))
    
    return DP[a][b]

def solution():
    global N, W, DP, works, result

    # village width
    N = int(input())

    # work number
    W = int(input())
    works = [(0, 0)]

    # N x N Cache
    DP = [[float('inf') for i in range(W + 1)] for j in range(W + 1)]
    for i in range(W):
        DP[i][W] = 0
        DP[W][i] = 0

    # input works
    for i in range(W):
        a, b = map(int, input().split(' '))
        works.append((a, b))

    # minimum total distances
    result = dfs(0, 0)
    print(result)

    # route
    trace_route(0, 0)

if __name__=="__main__":
    solution()

문제를 푸는 방법은 한 가지가 아니다, 라는 말이 있습니다. 이 문제도 다른 풀이 방법이 있을 것 같습니다. 틈나는대로 고민하며 다른 풀이를 떠올려 봐야겠습니다.