[Algorithm Problem] 팰린드롬? (BAEKJOON: 10942번)
Palindrome? (팰린드롬?)
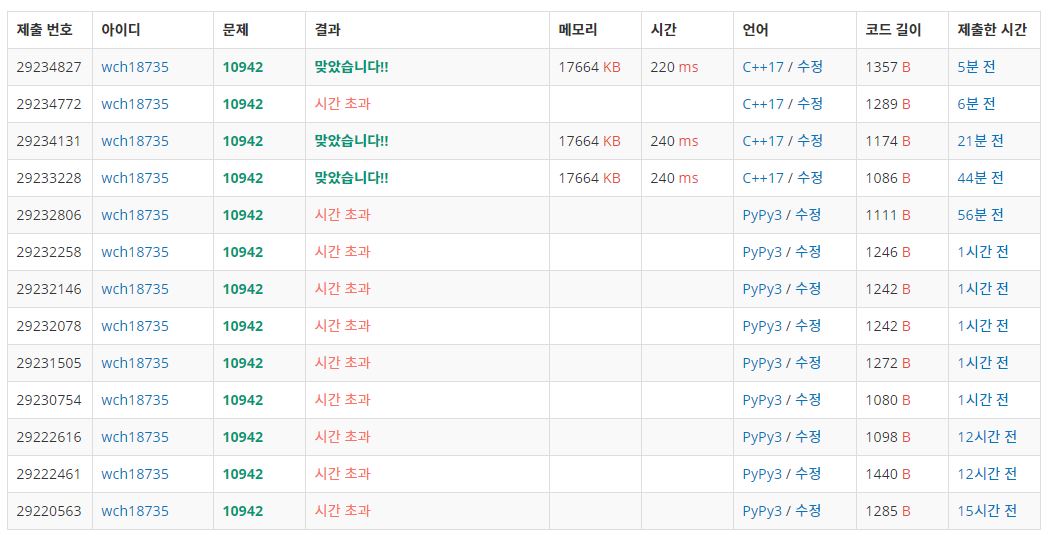
하루 종일 걸렸던 문제의 답은 C++ 였습니다. 시간초과인 Python 코드들을 C++로 고쳐서 문제를 푸니 모두 통과됐습니다.
팰린드롬이란 대칭을 이루는 단어 또는 수열을 말합니다. 동적 계획법에서는 문제를 푸는데 사용하는 부분 문제의 정답을 기록해두었다가 활용하여 연산을 빠르게 합니다. 저는 이 문제에서 부분 문제를 다음과 같이 정의했습니다.
- S, E 가 주어졌을 때, array[S] == array[E] 이고
- S + 1 ~ E - 1 까지의 부분이 모두 대칭이라면 Palindrome
여기서 S + 1 부터 E - 1을 미리 구해두면 S와 E가 주어졌을 때, 양 끝의 지점을 확인하고 내부가 팰린드롬을 이루는지만 확인하면 연산을 줄일 수 있습니다.
문제를 풀 때 다양한 방법이 가능합니다. 먼저 S, E를 입력받기 전 모든 펠린드롬 DP를 계산하는 방법과 그때마다 주어지는 값들을 계산하는 방법이 있습니다. 입력받기 전 모든 펠린드롬 DP를 계산하는 방법에도 위의 조건을 점화식처럼 활용하는 방법과 내부 펠린드롬을 확인하여 대칭이 아닐 때 모든 바깥쪽 펠린드롬을 제거하는 방법이 있습니다. 두 번째 방법은 에라토스테네스의 체를 떠올리시면 편할 것 같습니다.
요즘 Python의 편리함과 PyPy3 속도에 안심하고 있었는데, 다시 한 번 이런 문제를 만났습니다. 풀이에 확신이 있는데 시간초과가 나시는 분들은 C++ 로 바꾸어 제출해보시는 것을 권해드립니다.
Python은 이렇게 입출력 속도를 높여주는 것이 없나 찾아봐야겠습니다.
ios_base::sync_with_stdio(false);
cin.tie(NULL); cout.tie(NULL);
소스코드1: 조건을 점화식처럼 활용하는 방법
if __name__=="__main__":
N = int(input())
num_list = [0] + list(map(int, input().split(' ')))
# DP
IMPOSSIBLE = 0
POSSIBLE = 1
MATRIX = [[IMPOSSIBLE for i in range(N + 1)] for j in range(N + 1)]
# DP 초기화
# palindrome size: 1
for i in range(1, N + 1):
MATRIX[i][i] = POSSIBLE
# palindrome size: 2
for i in range(1, N):
if num_list[i] == num_list[i+1]:
MATRIX[i][i+1] = POSSIBLE
# palindrome size: 3 이상
for dif in range(2, N):
for left_point in range(1, N+1):
if left_point + dif > N:
break
# 양 끝이 매칭이고 안쪽이 모두 팰린드롬이면 팰린드롬
if num_list[left_point] == num_list[left_point + dif] and MATRIX[left_point + 1][left_point + dif - 1]:
MATRIX[left_point][left_point + dif] = POSSIBLE
else:
MATRIX[left_point][left_point + dif] = IMPOSSIBLE
M = int(input())
for m in range(M):
S, E = map(int, input().split(' '))
# 출력
print(MATRIX[S][E])
#include<iostream>
#include<algorithm>
using namespace std;
int num_arr[2001];
int dp_matrix[2001][2001];
int main(int argc, char* argv[])
{
ios_base::sync_with_stdio(false);
cin.tie(NULL); cout.tie(NULL);
// 수열 입력
int N;
cin >> N;
for (int i = 1; i <= N; i++) cin >> num_arr[i];
// dp_matrix 초기화
fill(&dp_matrix[0][0], &dp_matrix[2000][2000], false);
// palindrome 길이가 1일 때
for (int i = 1; i <= N; i++) dp_matrix[i][i] = true;
// palindrome 길이가 2일 때
for (int i = 1; i <= N - 1; i++)
{
if (num_arr[i] == num_arr[i + 1]) dp_matrix[i][i + 1] = true;
}
// palindrome 길이가 3 이상일 때
for (int dif = 2; dif <= N; dif++)
{
for (int left_point = 1; left_point + dif <= N; left_point++)
{
int right_point = left_point + dif;
if (num_arr[left_point] == num_arr[right_point] && dp_matrix[left_point + 1][right_point - 1])
{
dp_matrix[left_point][right_point] = true;
}
}
}
int M, S, E;
cin >> M;
for (int m = 0; m < M; m++)
{
cin >> S >> E;
cout << dp_matrix[S][E] << '\n';
}
return 0;
}
소스코드2: 바깥 펠린드롬을 제외하는 방법
if __name__=="__main__":
N = int(input())
num_list = [0] + list(input().split(' '))
# dp
NOT_VISIT = -1
POSSIBLE = 1
IMPOSSIBLE = 0
p_matrix = [[NOT_VISIT for i in range(N + 1)] for j in range(N + 1)]
for l in range(N):
# 펠린드롬 길이: +0 ~ +(N-1)
for S in range(1, N+1-l):
E = S + l
if S == E:
p_matrix[S][E] = POSSIBLE
else:
if p_matrix[S][E] == IMPOSSIBLE:
continue
# Not Visit (visit yet)
if num_list[S] == num_list[E]:
p_matrix[S][E] = POSSIBLE
else:
left_point = S
right_point = E
# 더 이상 볼 필요 없는 것들
while 0 < S and E <= N:
p_matrix[S][E] = IMPOSSIBLE
S -= 1
E += 1
M = int(input())
for m in range(M):
a, b = map(int, input().split(' '))
print(p_matrix[a][b])
#include<iostream>
#include<algorithm>
using namespace std;
int numArr[2001];
int palinDP[2001][2001];
const int not_visit = 2;
// MATCH WITH TimeOut4
int main(int argc, char* argv[])
{
ios_base::sync_with_stdio(false);
cin.tie(NULL); cout.tie(NULL);
int N;
cin >> N;
// array input
for (int i = 1; i <= N; i++) cin >> numArr[i];
// DP init
fill(&palinDP[0][0], &palinDP[2000][2000], not_visit);
for (int len = 0; len <= N; len++)
{
for (int lp = 1; lp + len <= N; lp++)
{
// right point
int rp = lp + len;
// palindrome length 1
if (lp == rp)
{
palinDP[lp][rp] = true;
continue;
}
// if visited
if (palinDP[lp][rp] != not_visit) continue;
// not visit
if (numArr[lp] == numArr[rp]) palinDP[lp][rp] = true;
else
{
int spread_lp = lp;
int spread_rp = rp;
while (0 < spread_lp and spread_rp <= N)
{
// exclude outer palinDP that is not need to be checked
palinDP[spread_lp][spread_rp] = false;
spread_lp -= 1; spread_rp += 1;
}
}
}
}
int M, S, E;
cin >> M;
for (int m = 0; m < M; m++)
{
cin >> S >> E;
cout << palinDP[S][E] << '\n';
}
return 0;
}
소스코드3: 재귀함수와 DP를 결합하여 문제마다 계산하는 방법
def palindrome(S, E):
global MATRIX, num_list
# 이전 결과값 이용
if MATRIX[S][E] is not NOT_VISIT:
return MATRIX[S][E]
# 종료 조건
if S == E:
MATRIX[S][E] = POSSIBLE
return POSSIBLE
elif E == S + 1:
# 짝수 판별
if num_list[S] == num_list[E]:
MATRIX[S][E] = POSSIBLE
return POSSIBLE
else:
MATRIX[S][E] = IMPOSSIBLE
return IMPOSSIBLE
# 연산
if num_list[S] == num_list[E] and palindrome(S + 1, E - 1) == POSSIBLE:
MATRIX[S][E] = POSSIBLE
return POSSIBLE
else:
MATRIX[S][E] = IMPOSSIBLE
return IMPOSSIBLE
if __name__=="__main__":
N = int(input())
num_list = [0] + list(map(int, input().split(' ')))
# DP
IMPOSSIBLE = 0
POSSIBLE = 1
NOT_VISIT = -1
MATRIX = [[NOT_VISIT for i in range(N + 1)] for j in range(N + 1)]
M = int(input())
for m in range(M):
a, b = map(int, input().split(' '))
if a == b:
print(1)
elif b == a + 1:
if num_list[a] == num_list[b]:
print(1)
else:
print(0)
else:
print(palindrome(a, b))
#include<iostream>
#include<algorithm>
using namespace std;
const int IMP = 0;
const int POS = 1;
const int NV = 2;
int numArr[2001];
int palinDP[2001][2001];
// MATCH WITH TimeOut6
int palindrome(int a, int b)
{
// use previous result
if (palinDP[a][b] != NV) return palinDP[a][b];
// End condition
if (a == b)
{
palinDP[a][b] = POS;
return POS;
}
else if (b == a + 1)
{
if (numArr[a] == numArr[b])
{
palinDP[a][b] = POS;
return POS;
}
else
{
palinDP[a][b] = IMP;
return IMP;
}
}
// check condition: each side match and inner array is palindrome
if (numArr[a] == numArr[b] && palindrome(a + 1, b - 1) == POS)
{
palinDP[a][b] = POS;
return POS;
}
else
{
palinDP[a][b] = IMP;
return IMP;
}
}
int main(int argc, char* argv[])
{
ios_base::sync_with_stdio(false);
cin.tie(NULL); cout.tie(NULL);
int N;
cin >> N;
// input sequence
for (int i = 1; i <= N; i++) cin >> numArr[i];
// init palinDP
fill(&palinDP[0][0], &palinDP[2000][2000], NV);
int M, S, E;
cin >> M;
// check palindrome
for (int m = 0; m < M; m++)
{
cin >> S >> E;
if (S == E) cout << 1 << '\n';
else if (E == S + 1)
{
if (numArr[S] == numArr[E]) cout << 1 << '\n';
else cout << 0 << '\n';
}
else {
// palindrome: check S ~ E is palindrome
cout << palindrome(S, E) << '\n';
}
}
return 0;
}

Leave a comment