[Algorithm Problem] 가장 긴 증가하는 부분 수열

May 16, 2021

Longest Increasing Subsequence (가장 긴 증가하는 부분 수열)

가장 긴 증가하는 부분 수열 문제는 동적 계획법을 이용해 푸는 대표적인 유형입니다. 이번 포스팅에서는 아래 문제들에 해당하는 개념들을 각각 다뤄볼 예정입니다.

먼저 가장 긴 증가하는 부분 수열의 개념에 대해서 알아보겠습니다. 위의 문제들에서 대표적으로 활용되는 예시입니다. 수열 A = {10, 20, 10, 30, 20, 50} 가 주어질 때, 가장 긴 증가하는 부분 수열는 아래와 같습니다.

A = {10, 20, 10, 30, 20, 50}

우리는 가장 긴 증가하는 부분 수열의 길이를 구할 수 있고, 그 길이에 대응되는 수열을 출력할 수 있습니다. 이번 포스팅에서는 $O(N^2)$, $O(N \ logN)$ 의 시간복잡도로 문제를 푸는 방법을 정리하겠습니다.

수열의 길이를 구하는 유형

$O(N^{2})$ 시간 복잡도

가장 긴 증가하는 부분 수열을 구성하는 원소를 구하기 전, 수열의 길이를 먼저 구해보겠습니다. 저는 위의 예시에서 가장 간단한 예부터 하나하나 증가시켜보며 Cache 값이 어떻게 변화하는 지를 확인하며 이해했습니다.

먼저 Cache를 DP[i]: i 번째까지 가장 긴 수열의 길이로 정의합니다. 아래와 같이 시작은 0번 인덱스를 가리킵니다. 이를 0부터 추가하는 이유는 무엇일까요? 문제에서는 최소 길이가 1이지만 만약 아무 배열도 주어지지 않을 때, 가장 긴 증가하는 부분 수열의 길이를 0으로 출력하기 위함입니다.

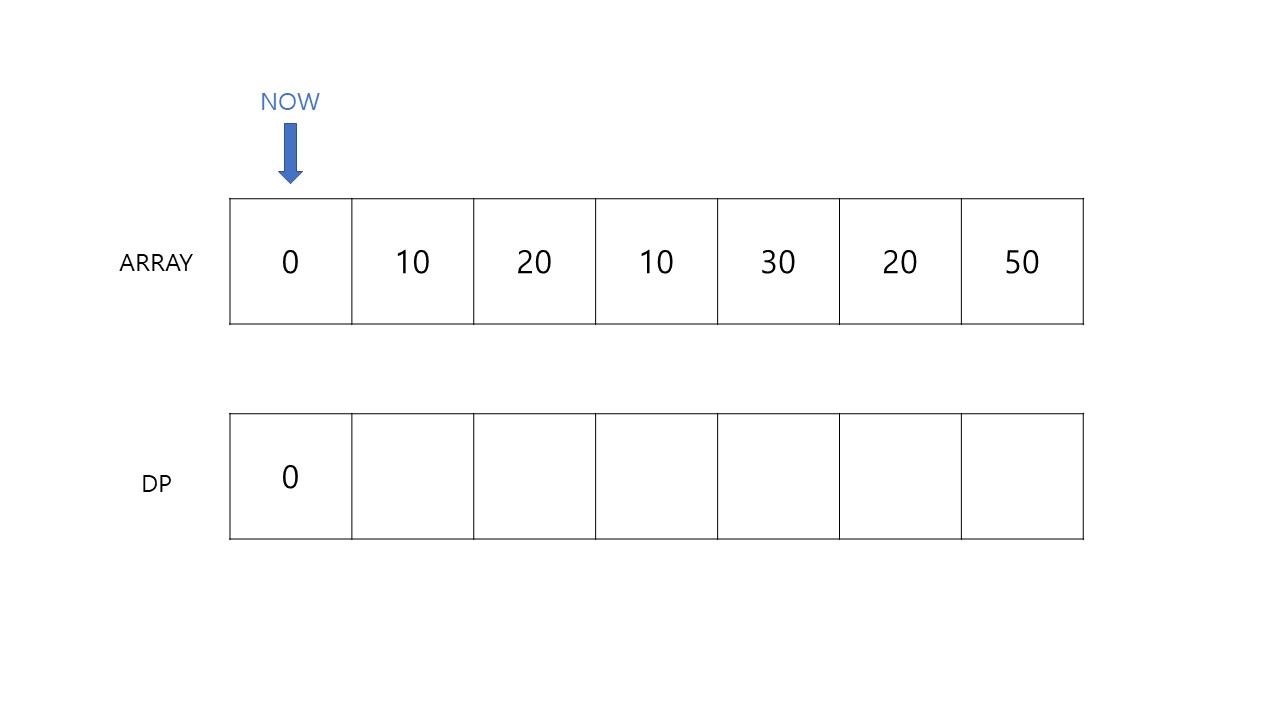
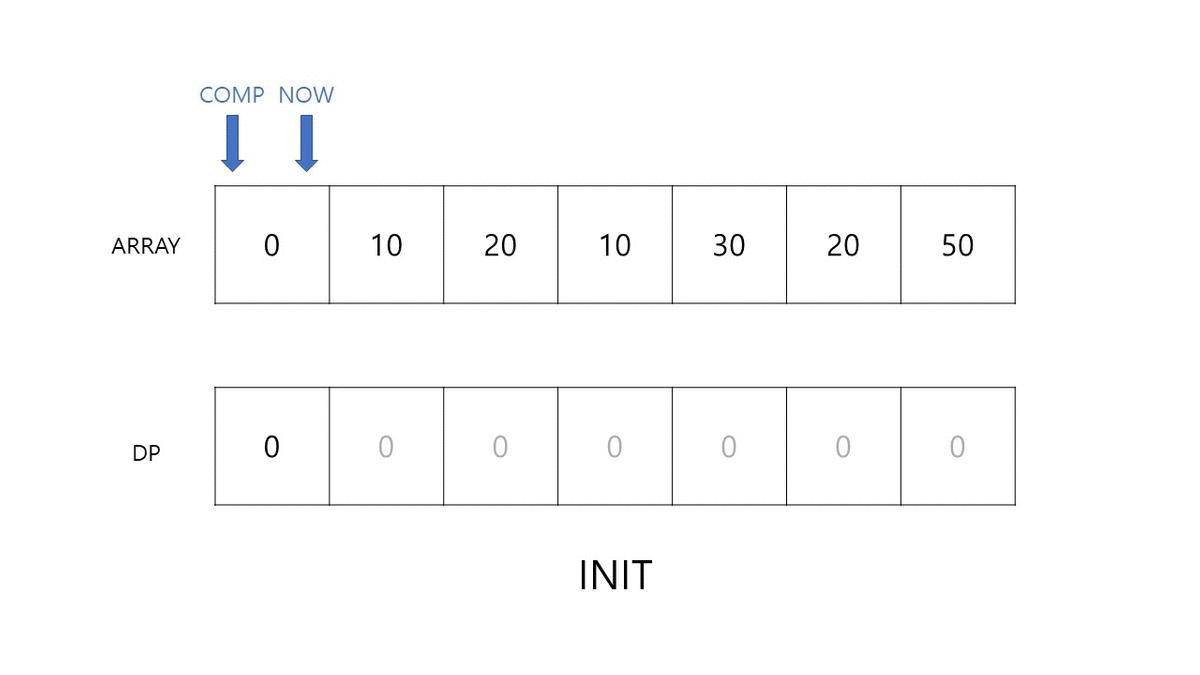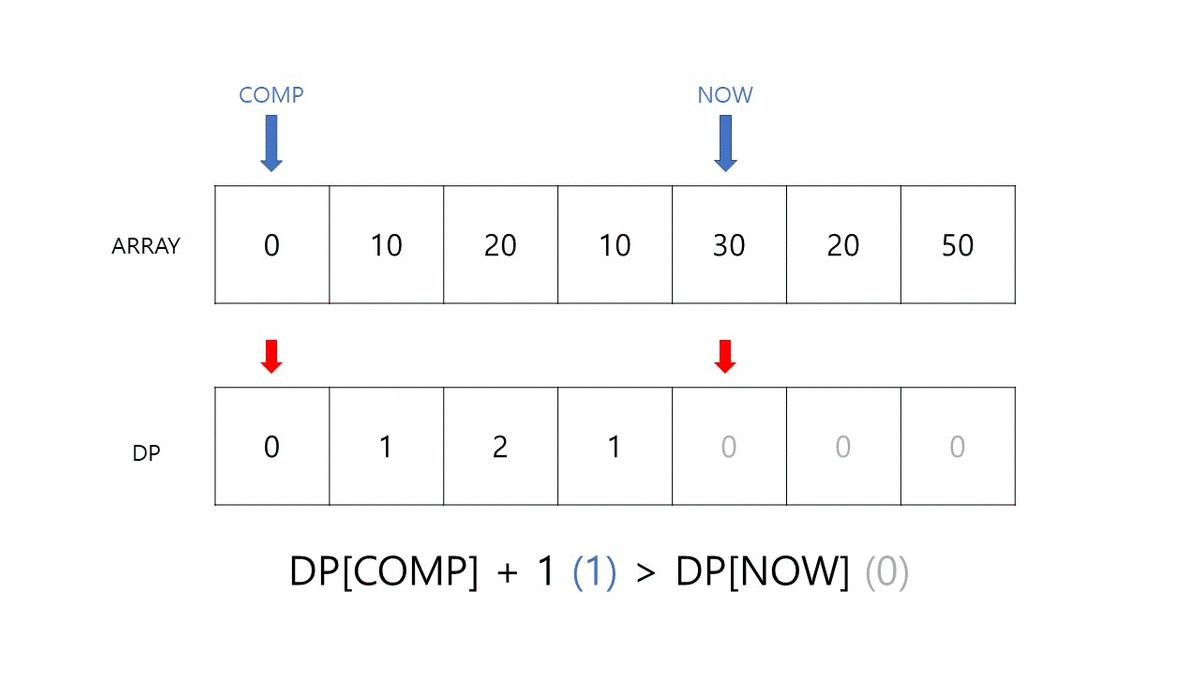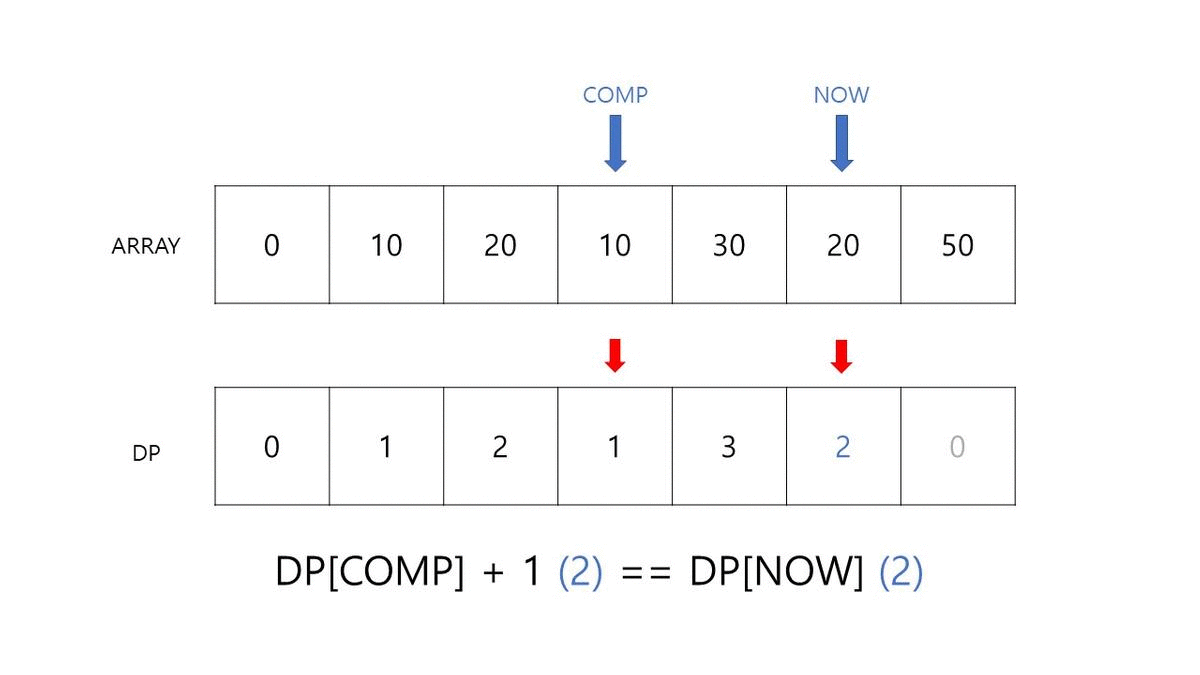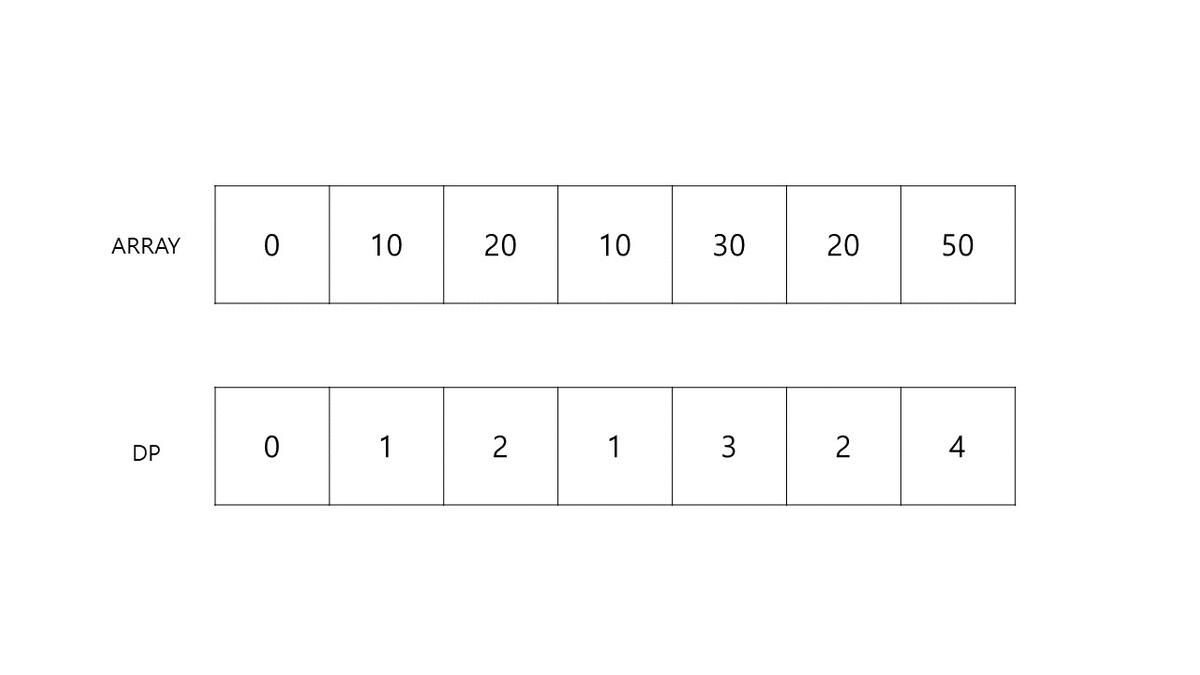
lis-1-1

NOW를 다음 칸으로 이동시킵니다. 그리고 아래의 과정을 거치며 DP를 업데이트 하겠습니다.

COMP가 가리키는 값이 NOW가 가리키는 값보다 큰지 확인합니다.
- NOW가 크다면 DP[COMP] + 1 값이 DP[NOW] 보다 큰지 확인합니다.
  - 더 크다면 DP[NOW] 값을 업데이트 합니다.
  - 작다면 순회를 계속합니다.
- COMP를 한 칸 옆으로 이동합니다.
COMP와 NOW가 같아지면 순회를 종료합니다.

INDEX 1번 칸에서는 COMP와의 비교가 한 번 일어납니다. 그리고 이때, ARRAY[COMP] 값이 0이고, DP[NOW] 값이 아직 아무것도 업데이트 되기 전이므로 이는 DP[COMP] + 1인 1이 됩니다.

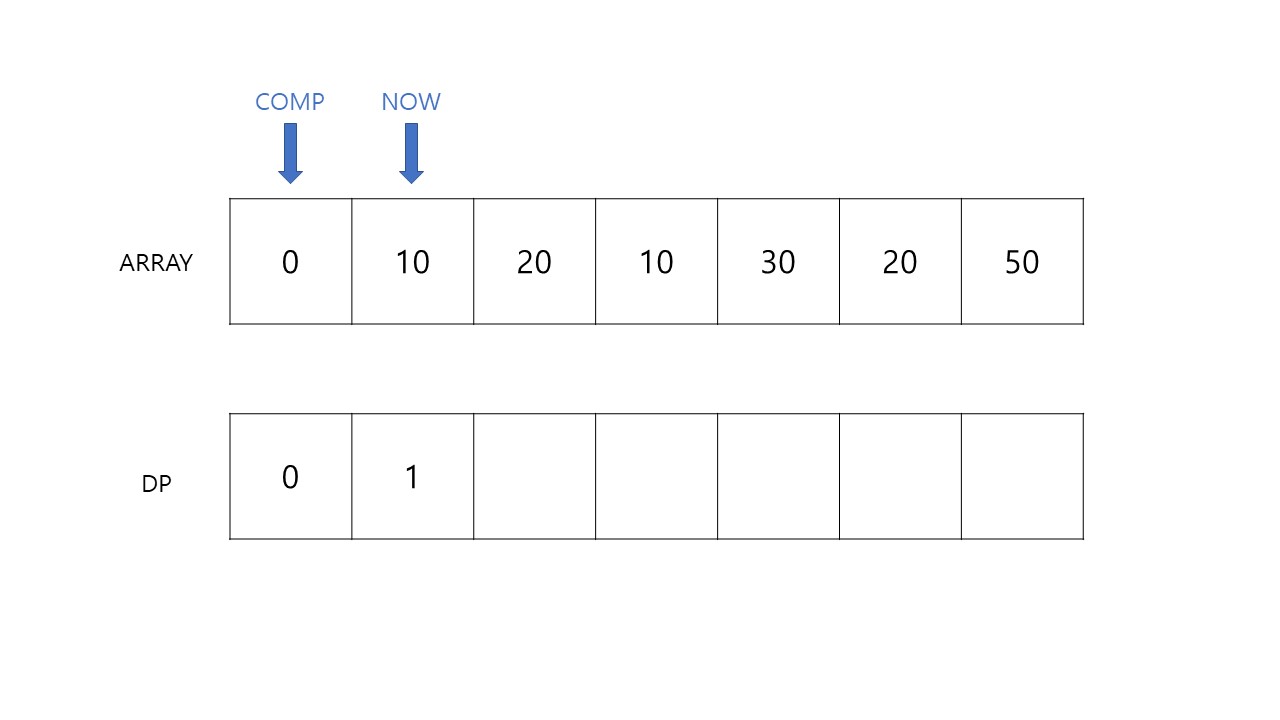
lis-1-1

이를 순서대로 진행하며 배열이 최신화되는 과정을 확인해보겠습니다. 아래 자료를 통해 각 DP가 어떻게 업데이트 되는지 눈으로 확인하면서 코드를 따라 보시면 조금 더 수월하게 이해할 수 있을 것 같습니다.

lis-1-1

if __name__=="__main__":
    N = int(input())

    arr = list(map(int, input().split(' ')))

    # dp
    dp = [1 for i in range(N)]
    dp[0] = 1

    # 오른쪽 최대 값
    for i in range(1, N):
        for k in range(0, i):
            # 현재 값이 arr[k]보다 크고
            # dp[i] < dp[k] + 1
            if arr[k] < arr[i] and dp[i] < dp[k] + 1:
                dp[i] = dp[k] + 1

    # 최대 값
    print(max(dp))

백준 11053번: 가장 긴 증가하는 부분 수열1은 수열 A의 크기 N이 $(1 \le N \le 1,000)$으로 주어집니다. 제곱의 시간복잡도에서도 시간제한 1초를 만족할 수 있습니다.

$O(N \ log{N})$ 시간 복잡도

그렇다면 백준 12015번: 가장 긴 증가하는 부분 수열2는 어떨까요? 이 문제에서 N은 $(1 \le N \le 1,000,000)$으로 주어집니다. 이는 시간복잡도 $O(N^2)$의 알고리즘으로는 시간제한 1초를 만족할 수 없습니다.

우리는 DP[i]: i 위치에서 가장 긴 수열의 길이를 이용해 문제를 풀었습니다. 이때, 우리는 굳이 모든 경우를 다 살펴볼 필요가 있었을까요? 이번에는 각 원소마다 현 상태의 LIS를 최신화하면서 몇 번째 인덱스에 위치할 수 있는지를 확인할 것입니다.

간단한 예를 들어보겠습니다. 수열 A = {10, 40, 20, 30} 이 주어졌을 때, 잠재적 LIS는 다음과 같은 과정을 거쳐 최종 길이 3를 출력합니다.

Initial LIS = [ ]
given element = 10, LIS = [10]
given element = 40, LIS = [10, 40]
given element = 20, LIS = [10, 20]
given element = 30, LIS = [10, 20, 30]

초기 LIS는 아무 값이 없는 빈 리스트입니다. 첫 번째 원소 10은 리스트의 0번 INDEX에 위치할 수 있습니다. 그 다음 40은 10보다 크기 때문에 LIS의 다음 원소에 포함될 수 있습니다. 즉, 리스트의 1번 INDEX에 위치할 수 있습니다.

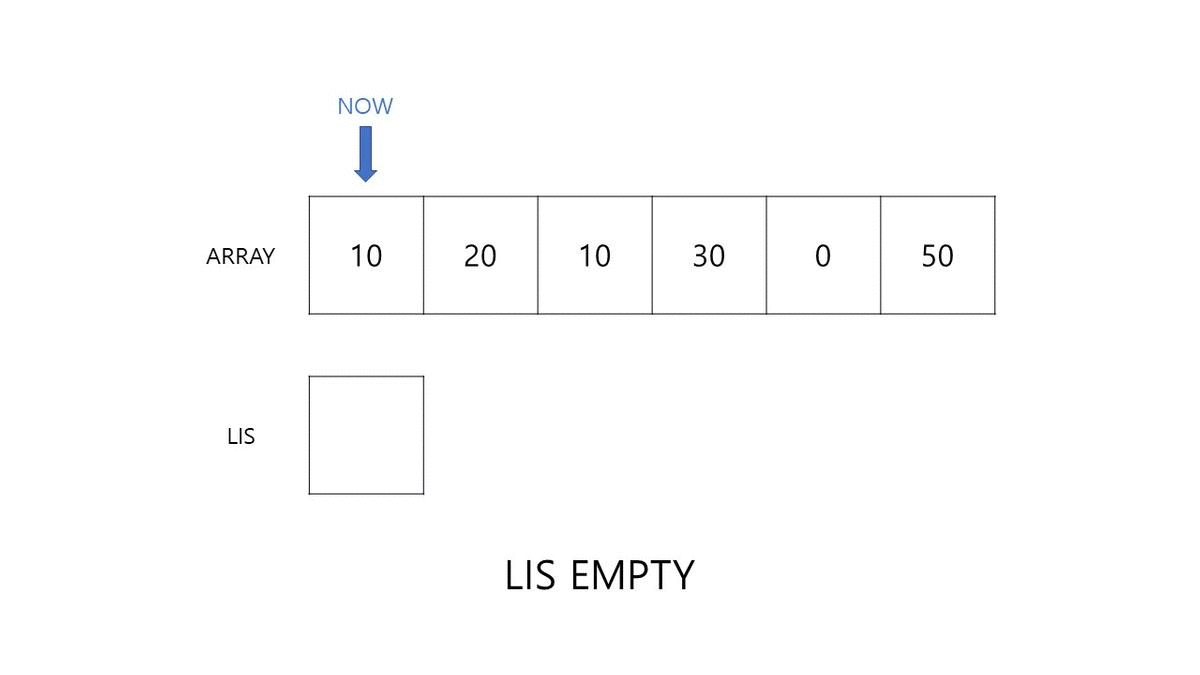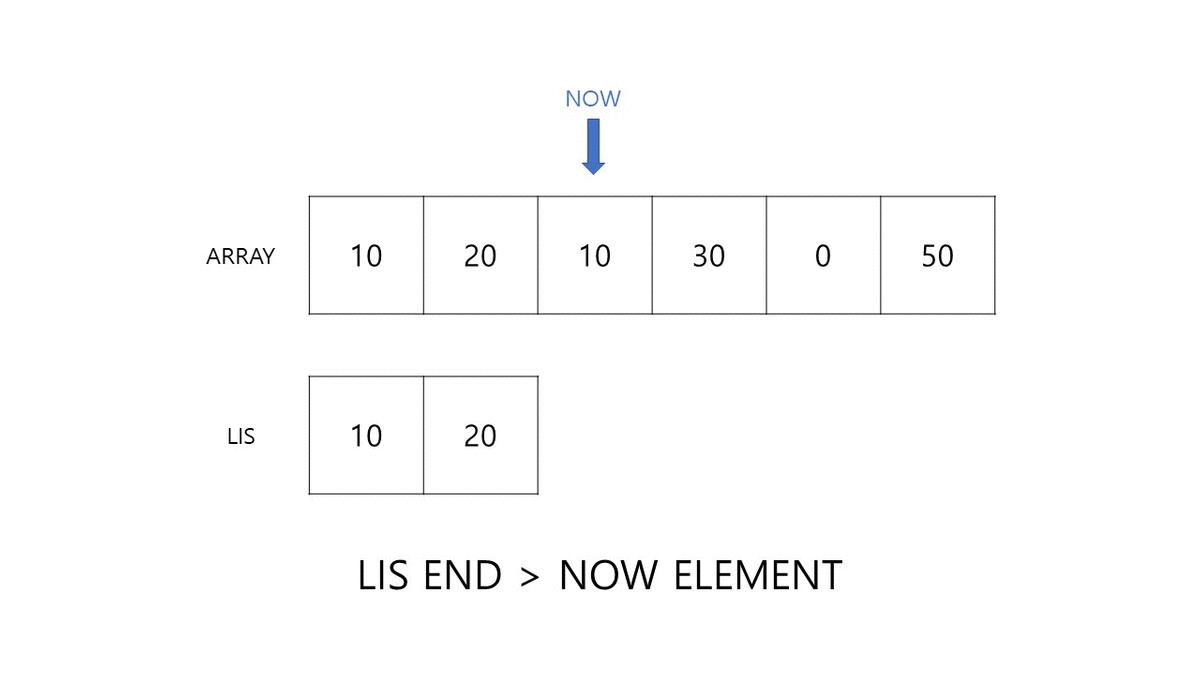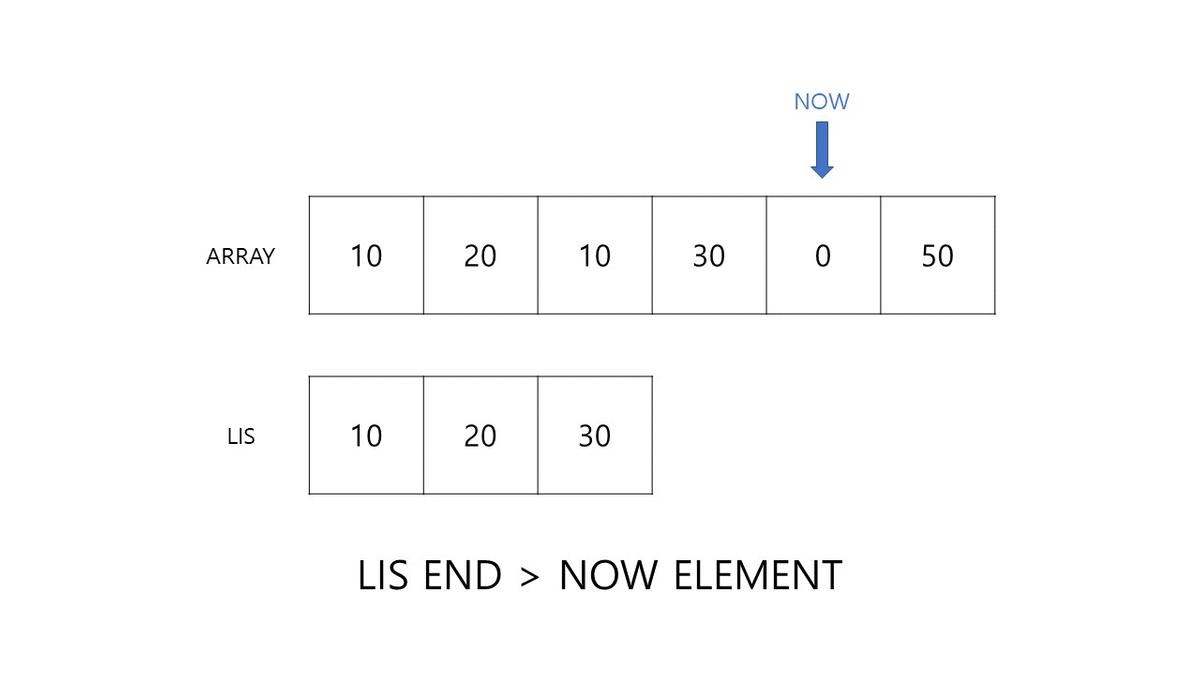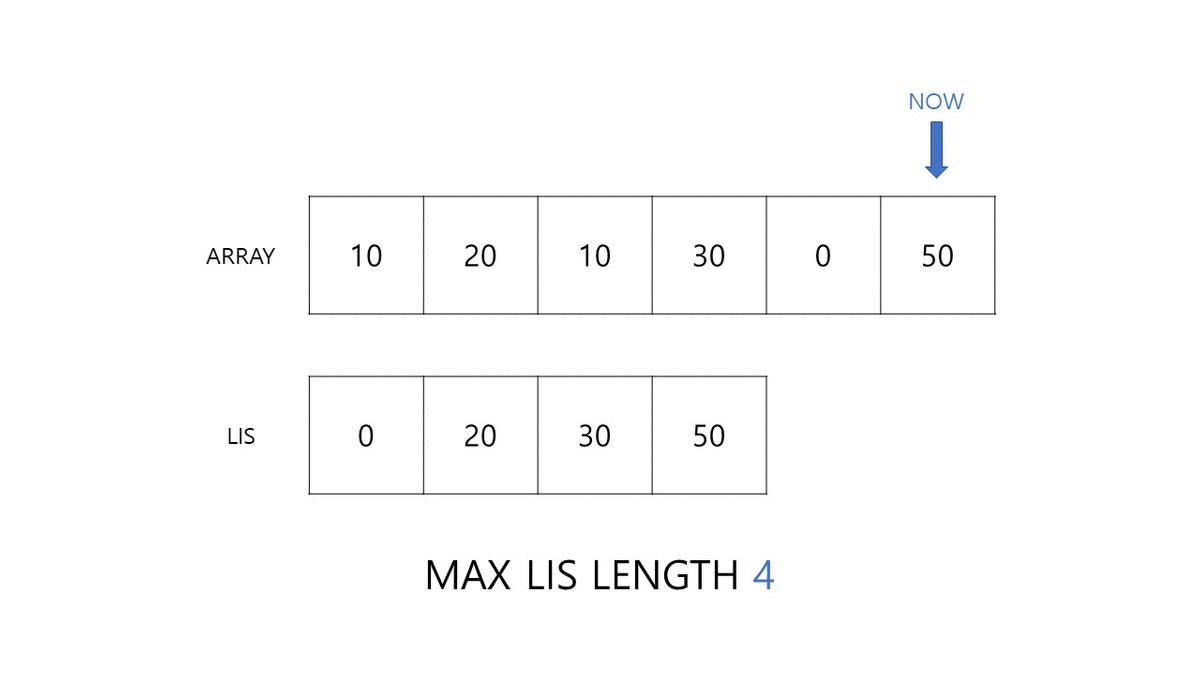
다음이 중요합니다. 세 번째 원소인 20은 10보다 크기 때문에 10의 위치인 0번 INDEX의 다음인 40을 대체하여 삽입될 수 있습니다. 만약 40이 아닌 15였다면? 20은 가장 끝보다 더 큰 크기이므로 끝에 추가될 수 있습니다.

이전에는 끝 값보다 값이 작다면 캐시를 업데이트하지 않았으나, 이번 알고리즘에서는 기존의 정보를 이용해 몇 번째에 위치할 수 있는지를 기록합니다. 끝으로 주어지는 30은 20보다 크기 때문에 뒤에 삽입될 수 있습니다.

위의 과정이 어떻게 시간복잡도를 줄일 수 있을까요? 그것은 바로 몇 번째 인덱스에 위치할 수 있는가를 찾는 과정에 있습니다. LIS는 오름차순으로 정렬되어있습니다. 그리고 이러한 배열에는 이분탐색과 같은 logarithmic search algorithm 을 사용할 수 있습니다.

실제 코드에서는 lower_bound를 이용해 그 인덱스를 구하고, 활용할 수 있습니다. 본인이 구현한 이분탐색 함수로는 제한시간을 만족하니, 라이브러리를 활용하면 간단하게 문제를 풀어보시고 본인이 스스로 구현하여 한 번 더 풀어보시는 것을 추천드립니다.

lis-1-1

from math import floor

def successor(arr, t):
    L = 0
    R = len(arr)

    while L < R:
        M = floor((L + R) / 2)

        # right most -> L need to move
        # L move when arr[M] < target
        # so, this compare equation get ==
        if arr[M] <= t:
            L = M + 1
        else:
            R = M

    if R == 0:
        return 0
    if arr[R-1] == t:
        return R - 1
    else:
        return R


if __name__=="__main__":
    N = int(input())

    arr = list(map(int, input().split(' ')))

    max_len_arr = [arr[0]]

    for i in range(N):
        if max_len_arr[-1] < arr[i]:
            max_len_arr += [arr[i]]
        elif max_len_arr[-1] == arr[i]:
            continue
        else:
            rm = successor(max_len_arr, arr[i])
            max_len_arr[rm] = arr[i]

    print(len(max_len_arr))

마지막 결과를 확인하시면 실제 LIS인 {10, 20, 30, 50} 대신 {0, 20, 30, 50}이 저장되어 있는 것을 확인하실 수 있으실 겁니다. 다음 차트에서는 LIS 길이와 그에 해당하는 실제 원소 값까지 구해보도록 하겠습니다.

수열의 길이와 원소를 구하는 유형

$O(N^{2})$ 시간 복잡도

백준 14002: 가장 긴 증가하는 부분 수열4 문제는 LIS의 길이와 함께 이를 구성하는 원소를 출력해야합니다. 어떻게 가능할까요? 현재까지 지나온 경로를 저장한다는 개념을 적용하면 가능합니다. NOW의 DP Cache가 최신화 될 때, (1) 이전 위치의 Cache 값과 (2) 현재 자신의 위치를 추가하여 지금까지 지나온 경로를 업데이트할 수 있습니다.

if __name__=="__main__":
    N = int(input())

    num_arr = list(map(int, input().split(' ')))

    # 경로 갱신 -> 업데이트 후 자기 위치 추가
    dp = [1 for _ in range(N)]
    dp_path = [[num_arr[i]] for i in range(N)]

    for i in range(1, N):
        for k in range(0, i):
            # arr[k]보다 크고 dp[i] < dp[k] + 1일 때 업데이트
            if num_arr[k] < num_arr[i] and dp[i] < dp[k] + 1:
                # dp 부분 최대 값 업데이트
                dp[i] = dp[k] + 1

                # 경로 추적
                dp_path[i] = dp_path[k] + [num_arr[i]]

    max_val = max(dp)
    print(max_val)

    max_idx = dp.index(max_val)
    print(*dp_path[max_idx])

간단한 예시를 들어보겠습니다. 수열 T = {10, 20, 10, 30} 가 주어졌을 때, LIS 길이와 이를 구성하는 요소를 구하는 과정을 살펴보겠습니다.

$j < i \ (1 \le i < N)$ 인 이중 for문을 구현합니다.
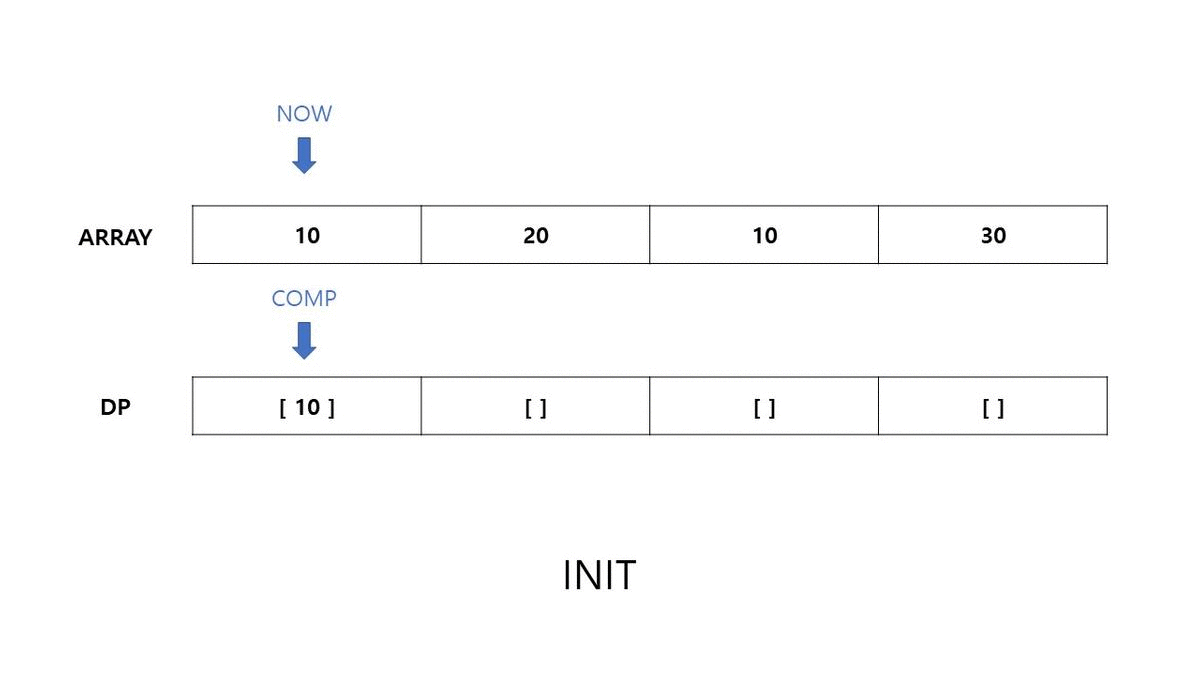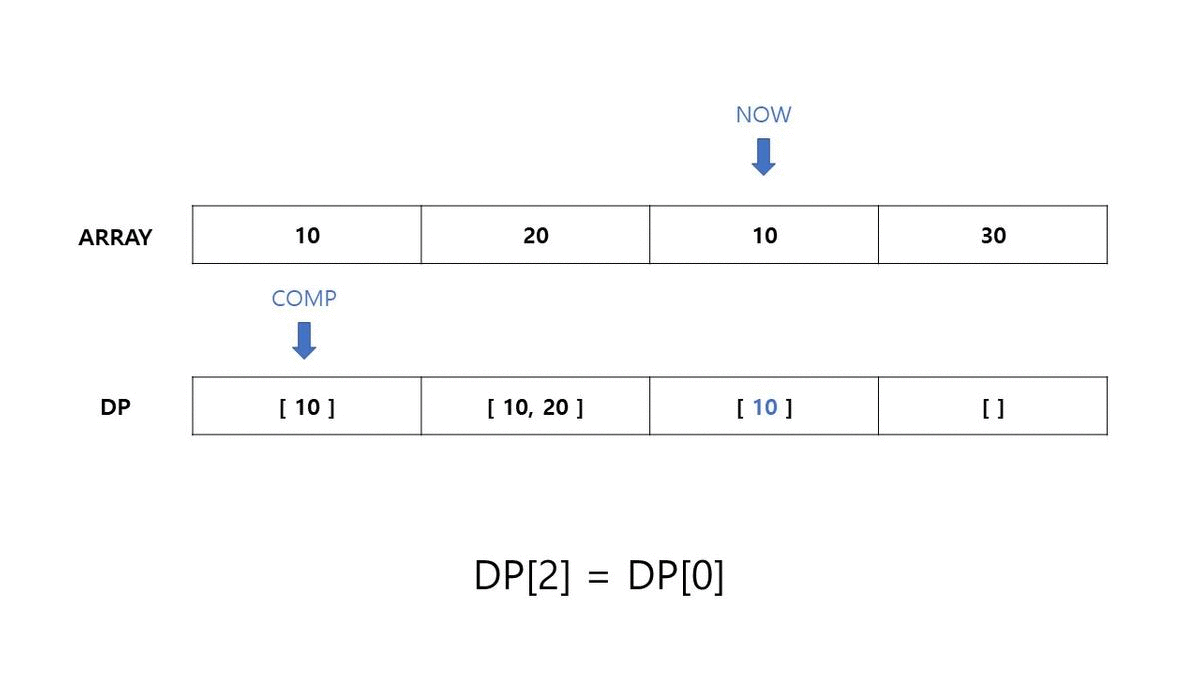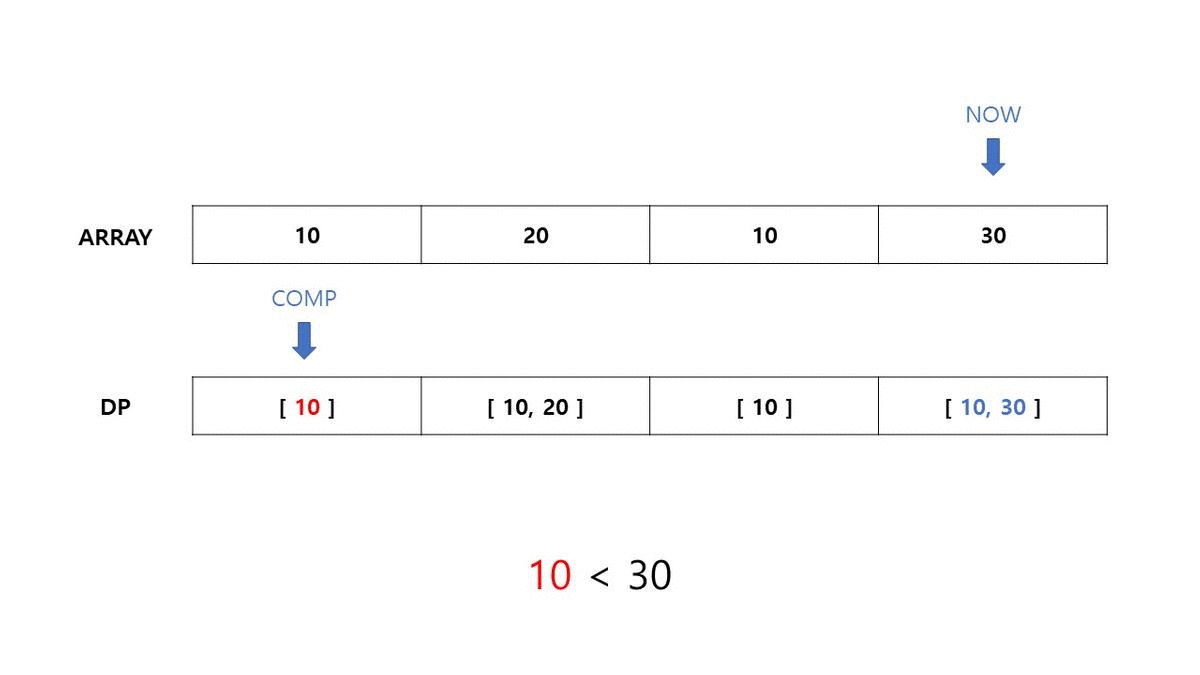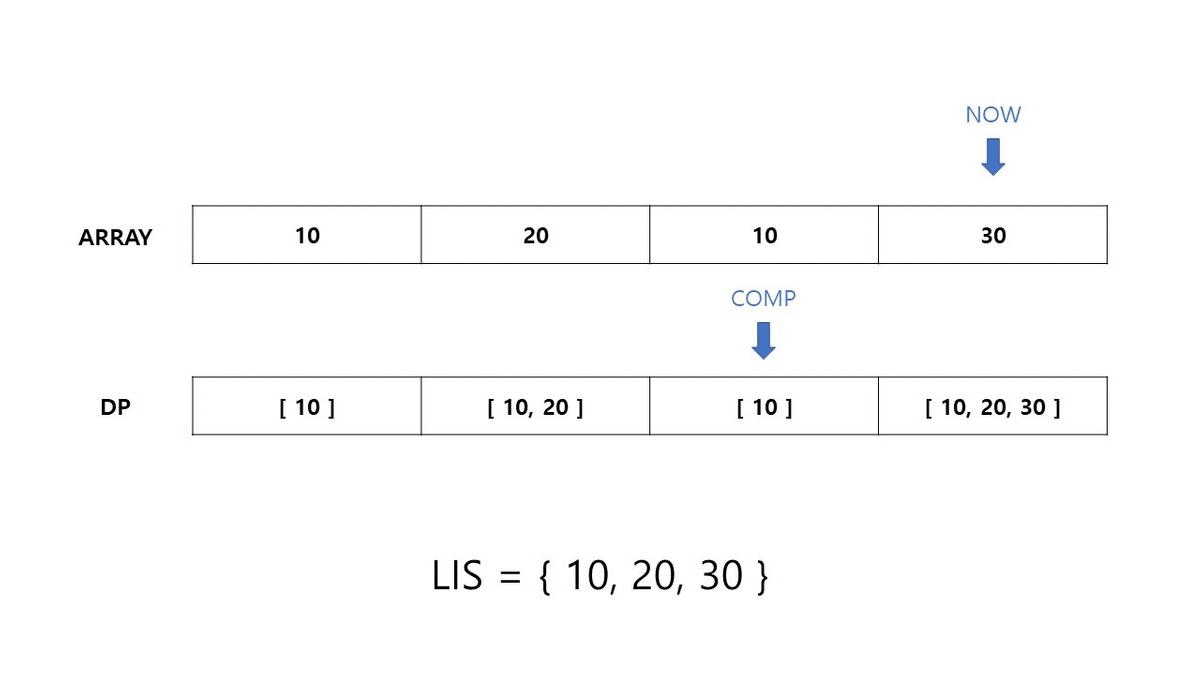
DP[0] 의 초기 값은 [ ARRAY[i] ] 로 설정합니다.
ARRAY[i] 의 현재 값과 DP[j] (현재까지 LIS) 의 마지막 값을 비교합니다.
마지막 값보다 현재 값이 크고, 현재 DP[i]의 길이가 더 작다면 DP[i] 를 DP[i] = DP[j] + [ ARRAY[i] ]을 통해 업데이트합니다.
같다면 이전 DP[j] 값을 그대로 삽입합니다.

lis-1-1

$O(N \ log{N})$ 시간 복잡도

백준 14003번: 가장 긴 증가하는 부분 수열5 에서는 N의 크기가 $0 \le N \le 1,000,000$ 으로 주어집니다. 이때는 전과 같은 방법으로 풀 수 없을 것 같습니다. 이전 풀이가 $O(N^2)$ 시간복잡도 방식에서 Cache의 성질을 변화시켜 문제를 풀었듯, $O(N \ logN)$ 시간복잡도 방식에서 Cache의 성질을 바꾸어 문제를 풀 수 있습니다.

이전 Log scale 풀이에서 LIS를 최신화하며 업데이트하던 것을 기억할 것입니다. 이때, 해당 원소가 LIS의 몇 번째에 추가되는지를 지속적으로 기록합니다. 그러면 (최대 INDEX) + 1이 LIS의 길이가 되고, 그 지점부터 이전까지 탐색하며 INDEX - 1에 해당하는 값들을 순차적으로 찾습니다.

Log scale 예제를 가지고 오겠습니다. 아래 그림의 DP_IDX는 현재 값이 LIS에서 위치할 수 있는 최대 값을 나타냅니다. 이제 DP_IDX 값이 0, 1, 2 인 값들을 순차적으로 표현하면 됩니다. 이때, 0으로 같을 가지는 원소가 3가지가 있습니다.

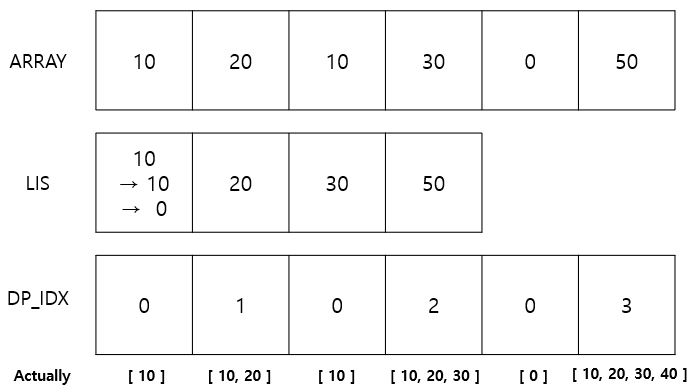
lis-1-1

이를 DP_IDX 값 == 1인 지점 이전이냐 이후냐로 판단할 수 있습니다. DP_IDX 값 == K 이후에 나오는 DP_IDX 값 < K 인 원소는 실제로는 아직 K + 1의 길이를 만족하지 못하는 LIS 상태이기 때문입니다. 이와 같은 발상을 응용하면 DP_IDX 값 == 1 인 지점이 여러 개일 때, 이는 DP_IDX 값 == 2인 지점 이전에 위치하는지로 판단할 수 있습니다. 그림의 Actually에서 이를 확인하실 수 있습니다.

#include<iostream>
#include<vector>
#include<algorithm>
#include<math.h>

using namespace std;

int arr[1000000];
struct pos {
	int value;
	int index = -1;
};
pos dp[1000000];

int main(int argc, char* argv[])
{
	ios_base::sync_with_stdio(false);
	cin.tie(NULL); cout.tie(NULL);

	int N;
	cin >> N;

	// input sequence
	for (int i = 0; i < N; i++)
	{
		cin >> arr[i];
		dp[i].value = arr[i];
	}

	// lis dp and init cache
	vector<int> lis;
	lis.push_back(arr[0]);
	dp[0].index = 0;
	int index_in_lis;
	for (int i = 1; i < N; i++)
	{
		if (lis.back() == arr[i]) continue;
		if (lis.back() < arr[i])
		{
			lis.push_back(arr[i]);
			dp[i].index = (int)lis.size() - 1;
		}
		else
		{
			index_in_lis = lower_bound(lis.begin(), lis.end(), arr[i]) - lis.begin();
			dp[i].index = index_in_lis;
			lis[index_in_lis] = arr[i];
		}
	}

	// lis length print
	cout << (int)lis.size() << '\n';

	// get lis element by possible index cache
	int length = (int)lis.size();
	vector<int> answer;

	for (int i = N - 1; i >= 0; i--)
	{
		if (dp[i].index + 1 == length)
		{
			answer.push_back(dp[i].value);
			length--;
		}

		if (length == 0) break;
	}

	// lis element print
	for (int i = (int)answer.size() - 1; i >= 0; i--) cout << answer[i] << ' ';

	return 0;
}

지금까지 LIS 유형을 정리해보았습니다. 부디 도움이 되었다면 좋겠습니다!

Share on

Twitter Facebook LinkedIn

1FeS

[Algorithm Problem] 가장 긴 증가하는 부분 수열

Longest Increasing Subsequence (가장 긴 증가하는 부분 수열)

수열의 길이를 구하는 유형

$O(N^{2})$ 시간 복잡도

$O(N \ log{N})$ 시간 복잡도

수열의 길이와 원소를 구하는 유형

$O(N^{2})$ 시간 복잡도

$O(N \ log{N})$ 시간 복잡도

Share on

Leave a comment

You may also enjoy

[HISTORY] BLOG CLOSE

[Java] LocalDate, LocalTime and LocalDateTime

[Design Pattern] Proxy Pattern (프록시 패턴)

[Design Pattern] Command Pattern (명령 패턴)