[Algorithm Problem] LCS2 (BAEKJOON: 9252번)

LCS2

이 문제는 동적계획법과 경로 추적 법을 결합해 푸는 문제였습니다. LCS (Longest Common Subsequence) 란 주어진 두 수열 또는 문자열에서 공통인 부분 중 가장 긴 것을 뜻합니다. LCS 1번 문제는 for 반복문을 이용한 방법으로 Knapsack 문제와 유사한 풀이 형태를 가졌습니다.

이번 문제 역시 Dynamic Programming Cache 배열을 만들고 이 값을 역추적하는 과정을 거쳐 LCS의 길이 뿐만 아니라 이를 구성하는 원소까지 구할 수 있었습니다.

제가 처음 생각했던 오답 코드는 아래와 같습니다. 업데이트를 하는 과정마다 DP에 LCS를 저장하는 방법입니다. 예시 문제는 풀 수 있었으나 Memory Out을 출력했습니다.

if __name__=="__main__":
    STR1 = input()
    STR2 = input()

    DP = [[[('', -1)] for i in range(len(STR1) + 1)] for j in range(len(STR2) + 1)]

    for i in range(len(STR1)):
        for j in range(len(STR2)):
            if STR1[i] == STR2[j]:
                if len(DP[i][j + 1]) < len(DP[i + 1][j]):
                    if DP[i + 1][j][-1][1] == i:
                        continue

                    DP[i + 1][j + 1] = DP[i + 1][j][:]
                    DP[i + 1][j + 1].append((STR1[i], i))
                else:
                    if DP[i][j + 1][-1][1] == i:
                        continue

                    DP[i + 1][j + 1] = DP[i][j + 1][:]
                    DP[i + 1][j + 1].append((STR1[i], i))

            else:
                if len(DP[i][j + 1]) < len(DP[i + 1][j]):
                    DP[i + 1][j + 1] = DP[i + 1][j][:]
                else:
                    DP[i + 1][j + 1] = DP[i][j + 1][:]

    answer = ''
    for CH, idx in DP[len(STR1)][len(STR2)][1:]:
        answer += CH
    print(len(answer))
    print(answer)

이 방법은 또한 마지막 인덱스를 고려할 때, 문제가 되었기 때문에 정답이 될 수 없었습니다. 이전 LCS 문제에서 DP Cache를 채우는 방법은 다음과 같습니다.

• str1[i]와 str2[j]가 같으면 DP[i + 1][j + 1]에 DP[i][j] + 1 값 대입
• str1[i]와 str2[j]가 같지 않다면 DP[i + 1][j + 1]에 max(DP[i][j + 1], DP[i + 1][j]) 값 대입

DP Cache에서 첫 행과 첫 열은 모두 0으로 초기화하기 때문에 문자열의 인덱스 + 1 값이 대응되는 위치입니다. DP[i + 1][j + 1] 값에 DP[i][j] + 1 값을 대입하는 것은 두 문자열의 끝에 같은 글자를 대입하는 것을 나타냅니다.

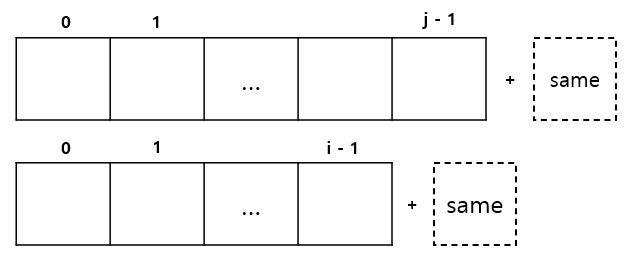
위의 규칙을 확인하면 다음을 알 수 있습니다. 공통의 원소가 나타나면 대각선 이전 값으로부터 +1을 취해줍니다. 반대로 같지 않은 경우에는 해당 위치에서 최대로 가지고 있을 수 있는 LCS의 길이를 비교해 최대 값으로 기록합니다.

따라서 특정한 길이에서 어떤 원소가 추가되었는지를 역으로 확인하며 이동하면 경로를 역추적 할 수 있습니다. 아래 표는 예제 입력에 대한 DP Cache 값입니다. 위와 왼쪽의 값과 모두 다를 때, 공통 원소가 추가된 것을 확인할 수 있습니다. 반대로 공통인자가 추가된 것이 아니라면 최대 값을 따라 이동합니다.

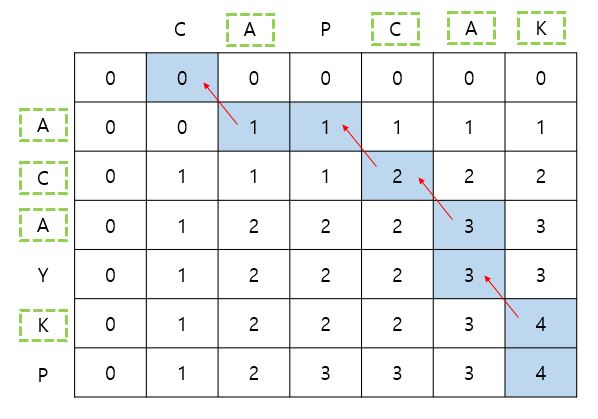
끝으로 추가된 값들을 모두 저장한 다음 역 순으로 출력해주면 답이 됩니다. 이때, 인덱스를 저장하는데, 두 문자열 중 어떤 것을 선택해도 괜찮습니다. 나중에 까먹을 때 쯤, 풀이없이 정답을 맞출 수 있을까 싶은 재밌는 문제였습니다!

def track(i, j):
    global DP

    answer = []

    while i != 0 or j != 0:
        # 현재 값이 왼쪽에서 온 것인지 오른쪽에서 온 것인지 확인
        current_val = DP[i][j]

        if DP[i-1][j] == current_val:
            i = i - 1
        elif DP[i][j-1] == current_val:
            j = j - 1
        else:
            # 일치할 때
            answer.append(i)
            i = i - 1
            j = j - 1

    return answer

if __name__ == "__main__":
    UPPER_STR = input()
    DOWN_STR = input()

    DP = [[0 for i in range(len(DOWN_STR) + 1)] for j in range(len(UPPER_STR) + 1)]

    for u_idx in range(1, len(UPPER_STR) + 1):
        for d_idx in range(1, len(DOWN_STR) + 1):
            if UPPER_STR[u_idx - 1] == DOWN_STR[d_idx - 1]:
                # 두 글자가 일치할 때
                # u_idx + 1, d_idx + 1 위치에 현재 값보다 +1
                DP[u_idx][d_idx] = DP[u_idx - 1][d_idx - 1] + 1
            else:
                # 글자가 일치하지 않을 때
                DP[u_idx][d_idx] = max(DP[u_idx][d_idx - 1], DP[u_idx - 1][d_idx])

    answer = track(len(UPPER_STR), len(DOWN_STR))

    for idx in answer[::-1]:
        print(UPPER_STR[idx - 1], end='')